|
|
|
|
Hilfen und Übungen in Mathematik
Ehemalige Chefredakteure von "Rainbow"
Interview mit
Aus dem
Leben einer Chefredakteurin ...
Referenzen & Aktivitäten von "Rainbow" ©
Peter Otto |
Lösungen: zu 1. P(2;1) und Q(5;4) I. 1 = 2² + 2p + q II. 4 = 5² + 5p + q
II. q = 4 – 25 -5p q = -21 - 5p
I = II: -3 – 2p = -21 – 5p → p = -6 → q = 9 → y = x² - 6x + 9 → S(-d;e) y = x² -6x + 9 + 3² - 3² → y = (x – 3)² → S(3;0) zu 2. P(1;0) und Q(4;-3) I. 0 = 1² + 1p + q
→ I = II: -1 – p = -19 – 4p → p = -6 → q = 5 → y = x² - 6x + 5 →
S(-d;e) y = x² -6x + 5 + 3² - 3²
à
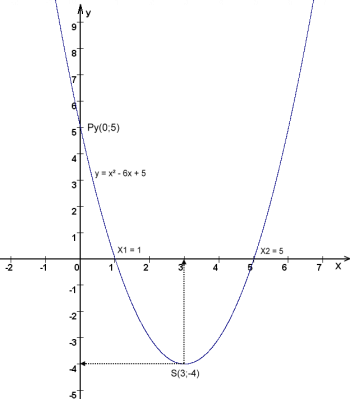
y = (x – 3)² - 4 0 = x² -6x + 5
→
x1/2 =
a) S(3;-4) zur Kontrolle:
|