|
Quadratische Funktionen
[Allgemeine
Form] [Sonderfälle] [y
= x²] [y
= ax² + c] [y
= (x + d)² + e] [Quadratische
Ergänzung]
[y = x² + px + q] [Nullstellen]
[Ermittlung
der Funktionsgleichung] [Übungen]
1. Begriff:
Die durch die Gleichung f(x) = ax² + bx + c
für a, b, c
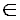 R und a ≠ 0 definierte Funktion f (x) heißt
quadratische Funktion oder
Funktion zweiten Grades.
R und a ≠ 0 definierte Funktion f (x) heißt
quadratische Funktion oder
Funktion zweiten Grades.
2.
Funktionsgleichung:
y = f(x) = ax² + bx + c
→
allgemeine Form der Gleichung einer quadratischen Funktion
↓
Die Zahlen a, b, c heißen Koeffizienten
der Funktion.
3. Sonderfälle
der allgemeinen Form:
(1) a = 1, b = 0 und c = 0 → y
= x² → Normalparabel
(2) c ≠ 0 und b = 0 → y = x² +
c → Verschiebung der
Normalparabel
entlang der y - Achse um c
(3) a > 0, c = 0 und b= 0
→ y = ax²
→ die um a gestreckte oder
gestauchte
Normalparabel
(4) a = 1, d ≠ 0 und e ≠ 0 → y
= (x + d)² + e →
Verschiebung der Normalparabel
entlang der y - Achse um e und
entlang der x- Achse um d
(5) a = 1, b = p und c = q → y
= x² + px + q →
Normalform einer quadratischen
Funktion
(6) a < 0, b ≠ 0 und c ≠
0 →
Parabel öffnet nach unten
4.
Die quadratische Funktion y = x²
Sonderfall der allgemeinen Form einer
quadratischen Funktion für a = 1 und b = 0 und c = 0
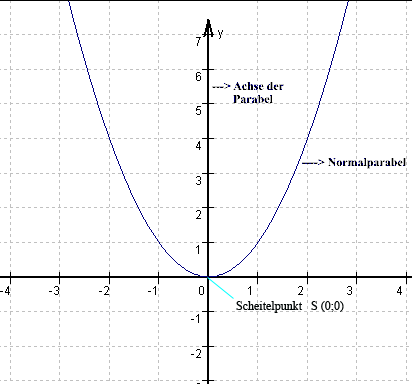
Wichtige Eigenschaften der Funktion y =
x²
(1) Definitionsbereich:
x 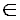 R
R
(2)
Wertebereich:
y
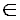 R und y
R und y
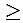 0
0
(3) f (0) = 0 ist der kleinste
Funktionswert.
(4) Im Intervall x
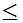 0 fällt das Bild der Funktion monoton.
0 fällt das Bild der Funktion monoton.
Im Intervall x
 0 steigt das Bild der Funktion monoton.
0 steigt das Bild der Funktion monoton.
(5) Das
Bild der Funktion ist eine quadratische Parabel.
→
Normalparabel
Das Bild liegt
axialsymmetrisch zur y - Achse.
5.
Die quadratische Funktion y =
ax² + c
Wie erhält man das Bild der
Funktion y = ax² + c aus dem Bild der Funktion y = x² (Normalparabel)?
(1) Die Normalparabel wurde um "c"
Einheiten entlang der y - Achse verschoben.
(2) Die Normalparabel wurde um den
Faktor "a" gestreckt bzw. gestaucht.
(3) Das Bild der Funktion y = ax² + c
ist eine quadratische Parabel.
(4) Die Scheitelpunktkoordinaten sind:
S (0 ; c)
(5) Wenn a < 0, dann öffnet die Parabel
nach unten.
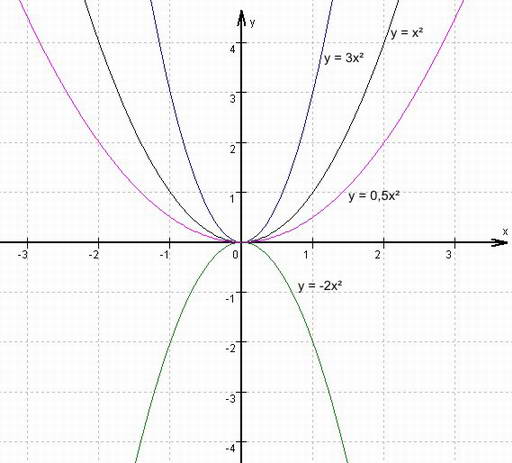
Fallunterscheidung
(1) a = 1
→
Normalparabel y = x²
(2) a > 1
→ Parabel gestreckt im
Vergleich zur Normalparabel y = x²
(3) 1 >
a > 0 →
Parabel gestaucht im Vergleich zur Normalparabel y = x²
(4) a < 0
→ Parabel an der x-Achse
gespiegelt (öffnet nach unten)
Beispiele:
|
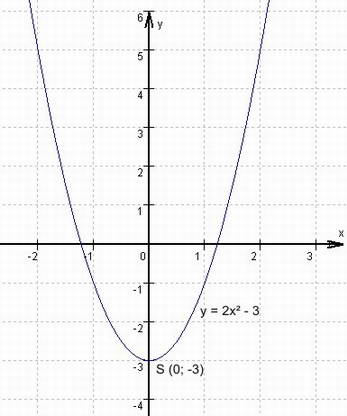
(1) y = 2x² - 3
 |
|
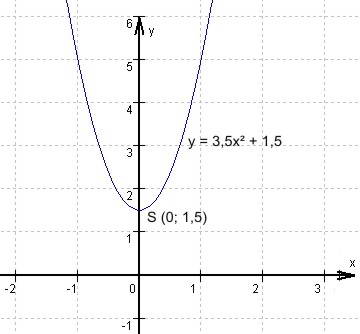
(2) y = 3,5x² + 1,5
 |
|
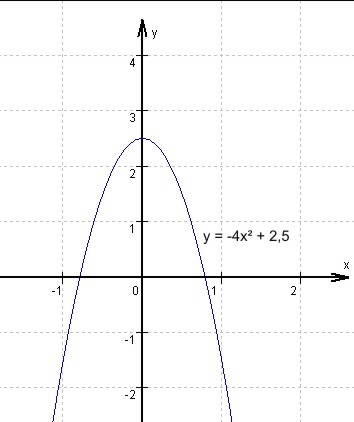
(3) y = -4x² + 2,5
 |
|
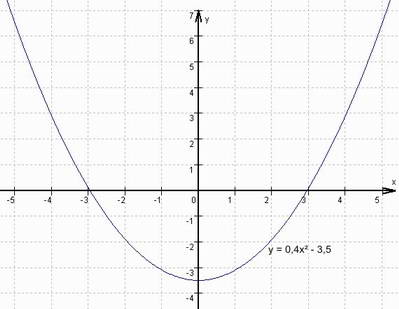
(4) y = 0,4x² - 3,5
 |
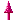
6.
Die quadratische Funktion y = (x+d)²
+
e (Scheitelpunktpunktform)
Ziel:
Grafische Darstellung der Funktion mit Hilfe der Normalparabel (Schablone)!
notwendig:
Scheitelpunktkoordinaten S (x;y)
→
S (-d;e)
Beispiel:
y = (x + 2)² - 1
→ d = 2 → -d = -2 ; e = -1 →
S (-2;-1)
 Das
Bild der Funktion y = (x + 2)² - 1 entsteht aus der Normalparabel (y = x²) durch
Verschiebung um -2 Einheiten (-d) entlang der x-Achse nach links und -1 Einheit
(e) entlang der y-Achse nach unten. Das
Bild der Funktion y = (x + 2)² - 1 entsteht aus der Normalparabel (y = x²) durch
Verschiebung um -2 Einheiten (-d) entlang der x-Achse nach links und -1 Einheit
(e) entlang der y-Achse nach unten.
7. Die Normalform
einer quadratischen Funktion: y = x² + px + q
Ziel:
Stellen Sie die Funktion y = x² + px + q mit Hilfe der Schablone der
Normalparabel grafisch dar! Ermitteln
Sie dazu aus der Normalform der quadratischen Funktion die Form y = (x + d)² +
e!
Bilden Sie dazu die quadratische
Ergänzung!
Lesen Sie die Scheitelpunktkoordinaten S (-d;e) ab.
Beispiel:
y = x² - 6x + 7
↓
quadratische Ergänzung zu (x² - 6x) →
Eine "quadratische Ergänzung" macht einen Term
bestimmen
der Form x² + p zu einem vollständigen Quadrat
der Form (x + p)²
y = x² - 6x + (3² - 3²) + 7
→ Man
ermittelt die "quadratische Ergänzung",
indem man das Quadrat von p/2 bildet!
↓
umformen
Damit
man die "quadratische Ergänzung" dem Term
bedenkenlos hinzufügen kann, muss man sie
gleichzeitig wieder subtrahieren!
Hier: (3² - 3²)
y = (x² - 6x + 3²) - 9 + 7
↓
vollständiges Quadrat angeben
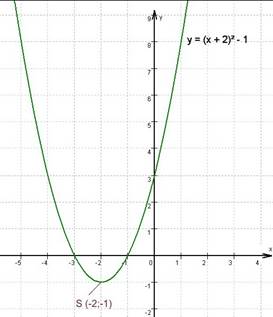
y = (x - 3)² - 2
(Scheitelpunktpunktform)
↓
Scheitelpunktkoordinaten S (-d;e) angeben
y = (x - 3)² - 2 → y = (x + d)² + e
→ d = - 3 →
- d = 3 und
e = - 2
→ S (3;-2)
Scheitelpunktkoordinaten
Weiteres (allgemeines) Beispiel:
Überführen Sie die Normalform einer quadratischen Funktion in eine Funktion mit
der Gleichung
y = (x + d)² + e! Geben Sie die Scheitelpunktkoordinaten S(-d;e) an!
y = x² + px + (p/2)
² - (p/2)² +q
→ y = (x + p/2)² - p²/4
+ q →
y =
(x + p/2)² + (- (p²/4 - q))
Beschreibung: d = p/2
und e = -(p²/4
– q) → e = - p²/4 +
q
Scheitelpunktkoordinaten:
S (-p/2;
q - p²/4)
Merke:
Die Differenz
p²/4
- q nennt man die Diskriminante
D der betreffenden
quadratischen Funktion.
Jede quadratische Funktion y = x² + px + q hat als Graph
eine zur Normalparabel kongruente Parabel mit dem Scheitelpunkt S (-p/2;
- p²/4 +
q) bzw. S (-p/2;
- D).
Jede Funktion y = x² + px + q nimmt also an der Stelle xS
= -p/2
ihren kleinsten Funktionswert yS
= -D an.
Für x
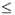 -p/2
ist die Funktion monoton fallend und für x -p/2
ist die Funktion monoton fallend und für x
 -p/2
monoton wachsend. -p/2
monoton wachsend.
Bei y = y0 =
q schneidet die Funktion die y-Achse und bei y = x0
(Nullstelle) die x-Achse.
8. Nullstellen der quadratischen Funktion y = x² + px
+ q
Merke:
Jede quadratische Funktion y = x² + px + q hat genau dann
Nullstellen, wenn für die Diskriminante D gilt:
D = p²/4
- q ≥ 0.
Fallunterscheidung:
|
D = p²/4 - q
|
ys = -D
|
Parabel y = x² + px + q
|
Funktion y = x² + px + q
|
|
D > 0
|
ys < 0
|
schneidet die x-Achse in zwei verschiedenen Punkten
|
hat genau zwei verschiedene Nullstellen
|
|
D = 0
|
ys = 0
|
berührt die x-Achse
|
hat genau eine Nullstelle
|
|
D < 0
|
ys > 0
|
hat keine gemeinsamen Punkte mit der x-Achse
|
hat keine Nullstellen
|
Beispielaufgabe:
Diskutieren Sie, ohne eine grafische Darstellung, die quadratische Funktion y =
x² + 4x + 1 hinsichtlich:
|
a) Scheitelpunktkoordinaten
|
b) Wertebereich
|
c) Definitionsbereich
|
|
d) Monotonieverhalten
|
e) Existenz von Nullstellen
|
f) kleinster Funktionswert (Minimum)
|
|
g) Schnittpunkt der Parabel mit der y-Achse
|
|
|
Lösung:
y = x² + 4x + 1 → y = (x + 2)² -
3
a) S(-2; -3)
b) y
 -3 -3
c)
-∞
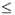 x x
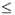 ∞ ∞
d) monoton fallend: x
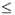 -2
und monoton steigend: x -2
und monoton steigend: x
 -2 -2
e) D = 3 → 2 Nullstellen
f) ymin = -3
g) y0 = 1
→ Sy(0;1)
Berechnung der Nullstellen der quadratischen Funktion y = x² + px + q
allgemein:
y = x² + px + q → y = 0
→ 0 = x² + px + q (quadratische Gleichung in
der Normalform)
→ Anwendung der allgemeinen Lösungsformel: x1/2
= -p/2
±
√(p/2)² - q
→ Lösungen der quadratischen Gleichung: x1
= -p/2 + √(p/2)² - q
x2 = -p/2 - √(p/2)²
- q
→ Nullstellen der zugehörigen quadratischen Funktion:
xo1 = -p/2 + √(p/2)²
- q
xo2 = -p/2 - √(p/2)²
- q
Beispiel:
Geben Sie die Nullstellen der quadratischen Funktion y = x² + 6x + 5 durch
Lösung der zugehörigen quadratischen Gleichung an!
y = x² + 6x + 5 → y = 0
→ 0 = x² + 6x + 5
→ Anwendung der allgemeinen Lösungsformel: x1/2
= -p/2
±
√(p/2)² - q
→ x1/2 = -6/2
±
√(6/2)² - 5
→ Lösungen der quadratischen Gleichung: x1
= -3 - 2 = -5
x2 = -3 + 2 = -1
→ Nullstellen der zugehörigen quadratischen Funktion:
xo1 = -5
xo2 = -1
→ Zur Kontrolle die graphische Darstellung der Funktion:
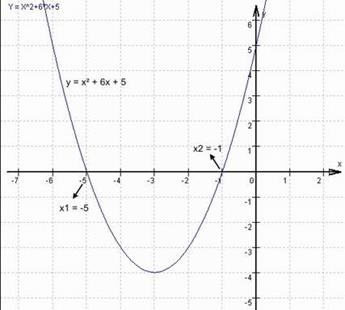
Merke:
Die Nullstellen der quadratischen Funktion y = x² + px + q entsprechen den
Lösungen der zugehörigen quadratischen Gleichung x² + px + q = 0.
9.
Ermittlung der Funktionsgleichung
y = x² + px + q bei zwei gegebenen Punkten
P und Q
Aufgabe:
Ermitteln Sie die Gleichung einer quadratischen Funktion in der Normalform y =
x² + px + q, wenn vom Funktionsbild zwei Punkte P und Q bekannt sind, die diese
Funktion erfüllen: P(5;6) und Q(2;3)! Formen Sie die ermittelte
Normalform in die Form y = (x + d)² + e um und geben Sie die
Scheitelpunktkoordinaten an! Stellen Sie die Funktion grafisch dar!
Lösung:
Punktkoordinaten von P und Q jeweils in die Funktionsgleichung (y = x² + px + q)
einsetzen
→ es ergibt sich ein lineares Gleichungssystem (2 Gleichungen mit 2 Unbekannten)
I. 6 = 5² + 5p + q
II. 3 = 2² + 2p + q
→ beide Gleichungen (z. B.) nach „q“ umformen und
dann gleichsetzen
I. q = -19 -5p
II. q = -1 – 2p
→ I = II:
- 19 -5p = -1 – 2p →
Gleichung nach p umformen → p = -6
→
p in Gleichung I oder II einsetzen und nach q umformen → q = 11
→
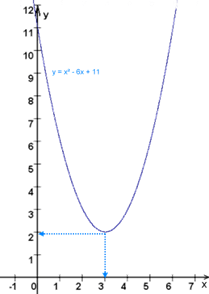
Funktionsgleichung: y = x² - 6x + 11
→ Scheitelpunktkoordinaten S(-d;e)
aus y = (x + d)² + e ermitteln
→
y = x² - 6x + 11
→
y = x² - 6x + 11 + 3² -
3³
→
y = x² - 6x + 3² + 11 –
3²
→
y = (x – 3)² + 2
→
S(3;2)
10. Übungen
1.
Ermitteln Sie die Gleichung einer quadratischen Funktion in der Normalform y =
x² + px + q, wenn vom Funktionsbild zwei Punkte A und B bekannt sind, die diese
Funktion erfüllen: A(2;1) und B(5;4)!
Formen Sie die ermittelte Normalform in die Form y = (x + d)² + e um und stellen
Sie die Funktion grafisch dar!
2.
Diskutieren Sie eine quadratische Funktion der Form y = x² + px + q, von
deren Graph lediglich zwei Punkte P(1;0) sowie Q(4;-3) bekannt sind,
hinsichtlich:
|
a) Scheitelpunktkoordinaten
|
b) Wertebereich
|
|
c) Definitionsbereich
|
d) Monotonieverhalten
|
|
e) Existenz (Angabe) von Nullstellen
|
f) kleinster Funktionswert (Minimum)
|
|
g) Schnittpunkt mit der y-Achse
|
Zeichnen Sie zur Kontrolle das Bild der gesuchten quadratischen
Funktion!
|
Lösungen
zurück |