|

Schülermosaik
Infothek "Liebe"
Infos für Schüler
Hilfen und Übungen in Mathematik
Hilfen und Übungen in Deutsch
Kaufmännischer Schriftverkehr
Tabellenkalkulation mit Excel
Referate & Dokumentationen
Kreativ schreiben
Poesiesprüche
Wer-Was-Wie-Warum?
Mode & Outfit
Berufe-Online
Impressum
Gondrams Rainbowpage
Magie & Mythen
Infothek "Liebe"
Entstehung von "Rainbow"
Ehemalige Chefredakteure von "Rainbow"
Interview mit
Christiane M.
(Mitbegründerin und 1. Chefredakteurin von "Rainbow")
Aus dem
Leben einer Chefredakteurin ...
(Marina K. - über 4 Jahre Chefredakteurin von
"Rainbow"
Referenzen & Aktivitäten von "Rainbow"

©
Peter Otto
schuelermosaik.de
|
Bewegung und Kongruenz
1.
Begriff der
Bewegung Eine Bewegung ist eine Abbildung der
Ebene auf sich. Man versteht darunter eine ...
... Verschiebung oder
... Drehung oder
... Spiegelung oder
... Nacheinanderausführung von Verschiebung, Drehung und
Spiegelung
2.
Arten der Bewegungen
Verschiebung: Für
die Verschiebung einer ebenen Figur sind die Angabe der
Verschiebungsrichtung und der Verschiebungsweite
notwendig.
Hier dargestellt durch den Verschiebungspfeil PP'.
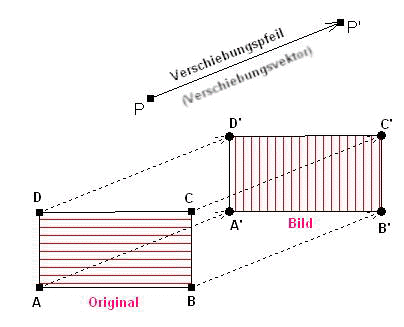
Eigenschaften der Verschiebung:
Spiegelung: Für die
Spiegelung einer ebenen Figur sind die Angabe der Lage und der
Richtung einer Spiegelgeraden notwendig.
Hier dargestellt durch die Gerade g(PQ).
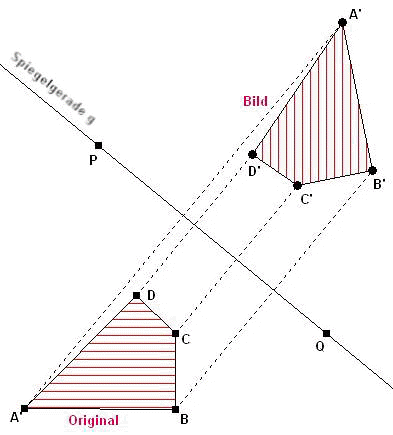
Eigenschaften der Spiegelung:
Drehung: Für die Drehung einer
ebenen Figur sind die Angabe eines Drehpunktes und
der Größe des Drehwinkels notwendig.
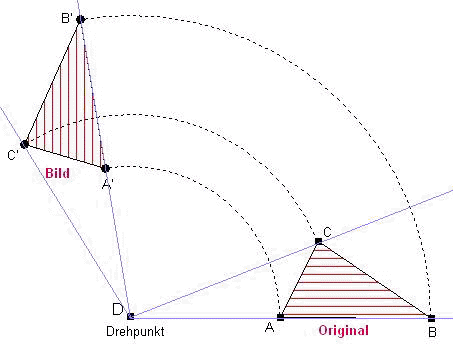
Nacheinanderausführung von Drehung, Verschiebung und Spiegelung:
- Drehung des Dreiecks ABC um D um Drehwinkel
- Verschiebung des Dreiecks A'B'C' in Richtung PP'
- Spiegelung des Dreiecks A''B''C'' an Geraden g(PQ)
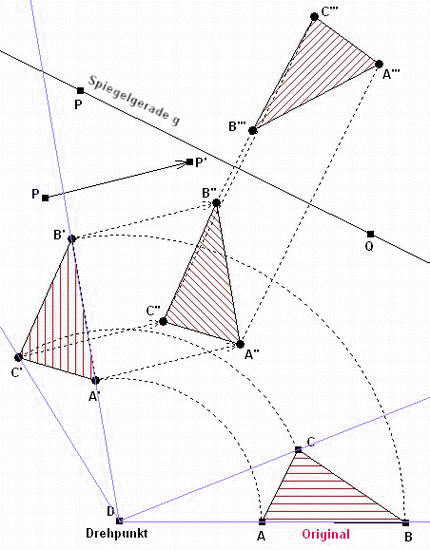
Übung-Bewegung01: Zeichnen Sie in ein
Koordinatensystem das Viereck A(3;8), B(5;9), C(5;12) und
D(2;12), die Gerade g durch die Punkte P(3;6) und Q(11;10)
sowie den Verschiebungspfeil von X(9;1) nach Y(15;1)!
-
Spiegeln Sie das Viereck ABCD an der
Geraden g(PQ)!
-
Verschieben Sie das entstandene Viereck
A'B'C'D' in Richtung des Verschiebungspfeiles XY um 6
Einheiten!
-
Drehen Sie das entstandene Viereck
A''B''C''D'' um den Drehpunkt B'' um 150°!
Lösung
3.
Eigenschaften der
Bewegungen
Alle Figuren, die durch Bewegungen auseinander
hervorgehen, sind deckungsgleich (kongruent).
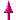
4.
Kongruenzsätze für Dreiecke
|
1. Satz: |
Wenn zwei Dreiecke in zwei Seiten und
dem eingeschlossenen Winkel übereinstimmen,
so sind sie zueinander kongruent. (SWS)
 |
|
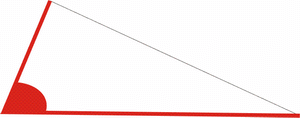
2. Satz: |
Wenn zwei Dreiecke in einer Seite und
den beiden anliegenden Winkeln
übereinstimmen, so sind sie zueinander
kongruent. (WSW)
 |
|
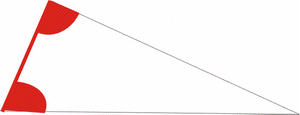
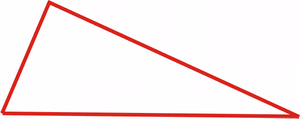
3. Satz: |
Wenn zwei Dreiecke in allen drei Seiten
übereinstimmen, so sind sie zueinander
kongruent. (SSS)
 |
|
4. Satz: |
Wenn zwei Dreiecke in zwei Seiten und
dem der größeren der beiden Seiten
gegenüberliegendem Winkel übereinstimmen, so
sind sie zueinander kongruent. (SSW)
 |
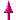
Übung-Bewegung02: Sind folgende Dreiecke
ABC mit dem Winkel
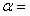  CAB und AB = c konstruierbar?
CAB und AB = c konstruierbar?
Begründen Sie Ihre Antwort, wenn es nicht möglich
sein sollte!
a)
a = 5,5 cm
b = 4,5 cm
c = 2,5 cm |
b)
a = 3,2 cm
b = 8,5 cm
c = 5,1 cm |
c)
a = 6,8 cm
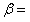 20° 20°
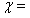 45° 45° |
d)
c = 8 cm
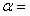 35° 35°
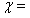 95° 95° |
e)
b = 7,5 cm
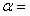 77° 77°
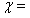 110° 110° |
f)
c = 8 cm
b = 3 cm
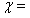 100° 100° |
g)
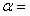 24° 24°
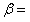 68° 68°
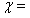 88° 88° |
|
Lösung
5.
Beweisführungen mit Hilfe der
Kongruenzsätze Wie ist ein Beweis aufgebaut?
|
Voraussetzung: |
Was wird vorausgesetzt? |
|
Behauptung: |
Was wird behauptet? |
| Beweis: |
Beweis der Behauptung mit Hilfe der Voraussetzung
sowie anderen schon bewiesenen Sätzen, Definitionen bzw. Regeln |
Beispiele:
| A1: |
Durch den Mittelpunkt M eines Kreises verlaufen zwei
Geraden g1 und g2, die nicht
senkrecht aufeinander stehen. Die Gerade g1
schneidet den Kreis in den Punkten A und B. Die Gerade g2
schneidet den Kreis in den Punkten C und D.
Verbindet man A mit C und B mit D, so entstehen die
Dreiecke MAC und MBD.
a) Entwerfen Sie eine Skizze!
b) Beweisen Sie mit Hilfe der
Kongruenzsätze, dass die Dreiecke MAC und MBD zueinander kongruent
sind! |
| Skizze: |
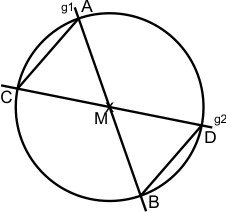 |
Beweis:
| Voraussetzung: |
siehe Skizze und Aufgabenstellung |
|
| Behauptung: |
Δ MAC
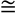 Δ MBD Δ MBD |
|
Beweis:
| Δ MAC |
|
Δ MBD |
Begründung |
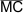 |
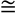 |
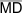 |
Die Radien im Kreis sind alle
gleich lang. |
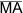 |
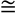 |
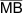 |
Die Radien
im Kreis sind alle gleich lang. |
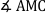 |
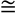 |
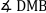 |
Scheitelwinkel sind gleich groß. |
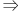 Nach dem Kongruenzsatz "SWS" gilt: Δ MAC
Nach dem Kongruenzsatz "SWS" gilt: Δ MAC
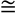 Δ MBD
w.z.b.w. Δ MBD
w.z.b.w.
| A2: |
Durch den Mittelpunkt M einer Strecke
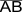 verlaufe die
Gerade g. Die Lote von den Punkten A und B auf diese
Gerade g haben die Fußpunkte C bzw. D. verlaufe die
Gerade g. Die Lote von den Punkten A und B auf diese
Gerade g haben die Fußpunkte C bzw. D.
a) Entwerfen Sie eine Skizze!
b) Beweisen Sie mit Hilfe der
Kongruenzsätze, dass die Dreiecke AMC und BMD zueinander kongruent
sind!
|
| Skizze: |
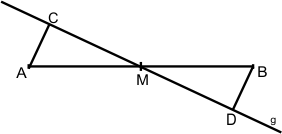 |
Beweis:
| Voraussetzung: |
siehe Skizze und Aufgabenstellung |
|
| Behauptung: |
Δ AMC
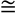 Δ
BMD Δ
BMD |
|
Beweis:
| Δ AMC |
|
Δ BMD |
Begründung |
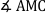 |
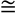 |
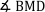 |
Scheitelwinkel sind gleich groß. |
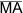 |
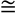 |
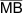 |
M ist
Mittelpunkt von
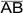 . . |
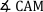 |
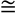 |
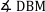 |
Wechselwinkel an geschnittenen
Parallelen (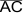
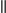
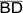 , da beides
Lote auf g sind) , da beides
Lote auf g sind) |
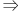 Nach dem Kongruenzsatz "WSW" gilt: Δ AMC
Nach dem Kongruenzsatz "WSW" gilt: Δ AMC
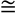 Δ
BMD
w.z.b.w. Δ
BMD
w.z.b.w.
 |







