|
Mengen und
Abbildungen
1
Mengen
Begriffe:
| Menge:
|
.. ist die Gesamtheit gleichartiger Objekte (mit gleichen Eigenschaften bzw. Merkmalen).
Es gibt endliche und unendliche Mengen. |
| Element einer Menge: |
... ist ein Objekt aus einer Menge ( ) ) |
|
Beispiele für Mengen und deren Elemente:
Mengen:
1. Menge aller Punkte einer Ebene
M1 (unendlich)
2. Menge der Eckpunkte eines Vierecks M2
(endlich)
3. Menge aller Primzahlen M3
(unendlich)
4. Menge aller geraden Primzahlen M4
(endlich)
5. Menge aller natürlichen Zahlen M5 =
N (unendlich)
6. Menge aller ganzen Zahlen M6 = Z
(unendlich)
7. Menge aller rationalen Zahlen M7 = Q
(unendlich)
8. Menge aller gebrochenen Zahlen M8 =
Q+ (unendlich)
9. Menge aller reellen Zahlen M9
= R (unendlich)
Element einer Menge:
M1 = {P1; P2;
P3; ...}
P2  M1
(Der
Punkt P2 ist eine Element der Menge M1) M1
(Der
Punkt P2 ist eine Element der Menge M1)
M2 = {A; B; C; D}
D  M2 M2
N = {0; 1; 2; 3; 4; 5; ...}
4  N
aber: -2 N
aber: -2
 N N
Z = {...; -2; -1; 0; 1; 2; 3; ...}
-1  Z Z
Begriffe:
| leere Menge: |
...
ist eine Menge, die kein Element enthält
(Bsp.: Menge der gemeinsamen Punkte zweier
Parallelen M =
 ) ) |
| Teilmenge:
|
...
enthält nur einen Teil der Objekte einer Menge (Untermenge
einer Menge ( ) )
M  N N
 m m
 N N
 n n
 M (m M (m
 M; n M; n
 N) N)
M ist Teilmenge von N, wenn alle Elemente von M auch Elemente von N
sind, aber nicht umgekehrt. |
|
geordnetes Paar: |
... eine Menge mit zwei
Elementen, deren Reihenfolge festgelegt ist {a; b} oder [a; b]
oder (a; b) |
|
Beispiele für Teilmengen:
Menge aller Primzahlen ist eine Teilmenge der natürlichen Zahlen
................... NP
 N N
Menge der natürlichen Zahlen ist eine Teilmenge der ganzen Zahlen
............... N
 Z Z
Menge der gebrochenen Zahlen ist eine Teilmenge der rationalen Zahlen
........ Q+
 Q Q
Menge der rationalen Zahlen ist eine Teilmenge der reellen Zahlen
.................. Q
 R R
Beispiele für geordnete Paare:
-
Formate (Maße) von Zeichnungen, Papier und Büchern
(a x b ...... Länge x Breite)
{210 mm x 297 mm}
→
Breite = 210 mm
{297 mm x 210 mm}
→
Breite = 297 mm
-
Angabe von Koordinaten im
Koordinatensystem (x; y)
2
Abbildungen
Arten von Abbildungen:
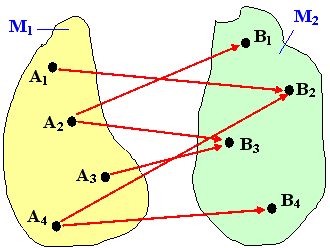
M1 ..... Originalmenge
M2 ..... Bildmenge
 |
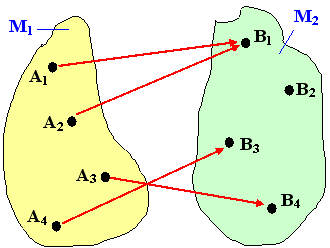 |
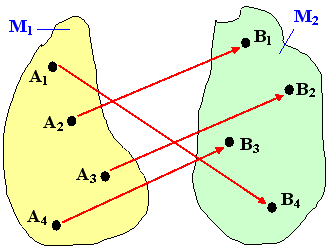 |
| mehrdeutige Abbildung |
eindeutige Abbildung |
eineindeutige Abbildung
(umkehrbar eindeutige Abbildungen) |
Eindeutige Abbildungen:
Jedem Originalpunkt wird genau ein
Bildpunkt zugeordnet.
Beispiele:
-
Verschiebung von Punkten, Strecken, Figuren, ....
-
Drehung, Spiegelung
-
Die Menge der natürlichen Zahlen wird eindeutig auf die
Menge der gebrochenen Zahlen zugeordnet. Es gibt keine Umkehrung!
(Jedem Element von N ist genau ein Element von Q+ zugeordnet.)
| |
N |
0 |
1 |
2 |
3 |
4 |
5 |
.... |
| |
|
↓ |
↓ |
↓ |
↓ |
↓ |
↓ |
|
| |
Q+ |
0 |
1/1 |
4/2 |
6/2 |
8/2 |
10/2 |
.... |
Durch die Eindeutigkeit der
Abbildung können geordnete Paare der Elemente der beiden Mengen angegeben
werden:
Beispiele:
N → Q+ :
[x; y] → [0; 0] , [1; 1/1]
, [2; 4/2] , [3; 6/2]
, [4; 8/2] , ...
nicht aber:
[14/2;
7]
Eineindeutige (umkehrbar eindeutige) Abbildungen:
Jedem Originalpunkt ist genau ein
Bildpunkt zugeordnet und umgekehrt hat jeder Bildpunkt genau einen
Originalpunkt.
Beispiele:
-
Die Menge der natürlichen Zahlen von 1 bis 2 (N1) wird
eineindeutig auf die
Menge der Teiler der Zahl 2 (T2) zugeordnet.
N1 = {1;2}
T2 = {1;2}
N1 ↔ T2
(Jedem Element von N1 ist genau ein Element von T2 zugeordnet
und umgekehrt.)
Mehrdeutige Abbildungen:
Mindestens einem Originalpunkt
sind mehrere
Bildpunkte zugeordnet.
Beispiele:
-
Verschiebung von Punkten, Strecken, Figuren, ....
-
Drehung, Spiegelung
-
Die Menge der natürlichen Zahlen wird eindeutig auf die
Menge der gebrochenen Zahlen zugeordnet. Es gibt keine Umkehrung!
(Jedem Element von N ist genau ein Element von Q+ zugeordnet.)
Abbildungen auf sich selbst:
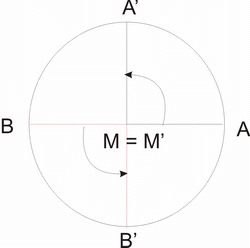 |
Drehung eines Kreises um den Mittelpunkt M A
→ A'
B → B'
M → M' |
-
Der Drehpunkt M wird auf sich selbst
abgebildet ( M = M').
-
Dreht man einen Kreis um seinen Mittelpunkt, so wird der
Kreis auf sich selbst abgebildet.
|