|
Beispielaufgabe:
Ein Rohbau wird
durch 12 Arbeiter in 15 Tagen erstellt, wenn die tägliche
Arbeitszeit 8 Stunden beträgt.
Wie viele Stunden müssen die Arbeiter täglich auf dem Bau sein,
wenn der Rohbau von 10 Arbeitern in 24 Tagen erstellt werden soll?
Lösung 1
(nach dem einfachen Dreisatz):
Ansatz:
12 Arbeiter
 15 Tage
15 Tage
 8 h
8 h
10 Arbeiter
 24 Tage
24 Tage
 x
xDer Dreisatz ist aus zwei Teilen
zusammengesetzt.
Beide Teile einzeln berechnen!
Für 12 Arbeiter gilt:
15 Tage
 8 h
8 h
 24
Tage 24
Tage
 x
x
(ungerader bzw. indirekter Dreisatz) |
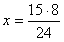 |
x = 5 h |
Für 10 Arbeiter gilt:
12 Arbeiter
 5 h
5 h
 10
Arbeiter 10
Arbeiter
 x
x
(ungerader bzw. indirekter Dreisatz) |
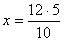 |
x = 6 h |
Antwort:
Die Arbeiter müssen täglich 6 Stunden auf
dem Bau sein, wenn der Rohbau von 10 Arbeitern in 24 Tagen erstellt
werden soll.
Lösung 2
(nach dem vereinfachten Schema des zusammengesetzten Dreisatzes):
Ansatz:
12 Arbeiter
 15 Tage
15 Tage
 8 h
8 h
10 Arbeiter
 24 Tage
24 Tage
 x
xBeide Dreisätze sind ungerade.
1. Dreisatz:
Für 12 Arbeiter gilt ...
2. Dreisatz: Für 10
Arbeiter gilt ...
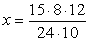 |
x = 6 h |

Aufgabe 2:
Ein Wanderer läuft 224 Kilometer in 7 Tagen,
wenn er täglich 8 Stunden unterwegs ist.
In wie viel Tagen legt der Wanderer 216 Kilometer zurück, wenn er
täglich nur 6 Stunden unterwegs ist?
Lösung 1
(nach dem einfachen Dreisatz):
Ansatz:
224 km
 7
Tage 7
Tage
 8 h
8 h
216 km
 x
x
 6 h
6 h
Der Dreisatz ist aus zwei Teilen zusammengesetzt.
Beide Teile einzeln berechnen!
Für 224 km gilt:
7 Tage
 8 h
8 h
x
 6 h
6 h
(ungerader bzw. indirekter Dreisatz) |
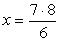 |
x = 9,333... Tage |
Für 216 km gilt:
224 km
 9,333... Tage
9,333... Tage
 216
km 216
km
 x
x
(gerader bzw. direkter Dreisatz) |
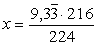 |
x = 9 Tage |
Antwort: Der Wanderer legt in 9 Tagen
die Strecke von 216 km zurück, wenn er täglich 6 Stunden unterwegs
ist.
Lösung 2
(nach dem vereinfachten Schema des zusammengesetzten Dreisatzes):
Ansatz:
224 km
 7 Tage
7 Tage
 8 h
8 h
216 km
 x
x
 6 h
6 h
Der 1. Dreisatz ist ungerade und der 2.
Dreisatz ist gerade.
1. Dreisatz:
Für 224 km gilt ...
2. Dreisatz: Für 216
km gilt ...
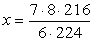 |
x = 9 Tage |
Übungsaufgaben
 |