|
Einführung in die Bruchrechnung
1. Der Bruchbegriff
 |
Die Tafel unter drei Kindern aufteilen! |
→ |
 |
|
 |
 |
→ Die
Schokoladentafel wird zer"brochen" →
Jedes Kind erhält einen "Bruchteil".
→ Wenn die Tafel
aus 15 Stücken Schokolade bestand, erhält
jedes Kind 5 Stücke.
→ Jedes Kind erhält
also 5 von 15 Stücken Schokolade!
Allgemein:
|
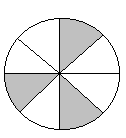
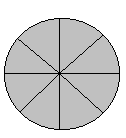
8 gleiche (Kreis)-Teile |
→
3 Teile von 8 Teilen hervorgehoben
→ 3 von 8 → 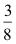
 |
|
(ein ganzer Kreis) |
|
Bruchbegriff:
Ein Bruch ist ein Teil vom Ganzen.
Übungsaufgaben
zum Bruchbegriff
2. Arten von Brüchen
Gemischte Zahlen und
unechte Brüche
Begriffe:
unechter Bruch:
Bruch, bei dem gilt: Zähler
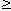 Nenner → z. B.: 9/4
oder 8/8
Nenner → z. B.: 9/4
oder 8/8
gemischte Zahl: ein
Ausdruck aus einer ganzen Zahl und einem echten Bruch
→ z.
B.: 3½ = 3 + ½
a) Schreibe einen unechten Bruch als gemischte
Zahl!
|
13/8
→ |
  |
→
1 + 5/8
→
1 5/8 (Schreibweise) |
Zusammenfassung:
13/8
=
1 5/8
|
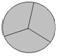
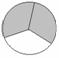
14/3 |
→ |
  |
→
1 + 1 + 1 + 1 + 2/3
= 4 + 2/3
=
4 2/3 |
Zusammenfassung:
14/3
=
4 2/3
Kürzer:
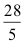 → Wie oft passt die 5 ganzzahlig in 28?
→
→ Wie oft passt die 5 ganzzahlig in 28?
→
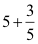 →
5 3/5
→
5 3/5
Zusammenfassung:
28/5
=
5 3/5
45/4 = 11 + ¼ =
11 ¼
Zusammenfassung:
45/4
=
11 1/4
b) Schreibe eine gemischte Zahl als unechten Bruch!
| 4 1/3 = 1 + 1 + 1 + 1 +
1/3
= 3/3 + 3/3 + 3/3
+ 3/3 + 1/3
↓ |
|
|
|
= 13/3 |
Kürzer:
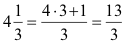
Einfache Übungsaufgaben:
Arten von Brüchen
1. Ordne folgende Brüche in echte
und unechte!
5/9 , 27/18
, 17/8 , 13/20 , 7/7
, 1/9 , 7/5 , 5/8
, 12/9 , 8/11 , 18/18
, 100/25 , 26/1000
2. Verwandle folgende Brüche in ganze
oder gemischte Zahlen!
7/5 , 8/4
, 15/9 , 12/6 , 23/4
, 23/9 , 18/3 , 16/5
, 0/13 , 19/2 , 18/5
, 78/7 , 15/0 , 96/12
3. Verwandle folgende gemischte Zahlen in
unechte Brüche!
2 ½ , 3 ¾ , 1 5/6 , 4
8/9 , 5 2/5 , 9 5/8
, 7 2/3 , 6 11/12 , 7 13/15
, 11 4/5
Lösungen
3.
Rechnen mit Brüchen
3.1 Vergleichen, Addieren
und Subtrahieren von Brüchen
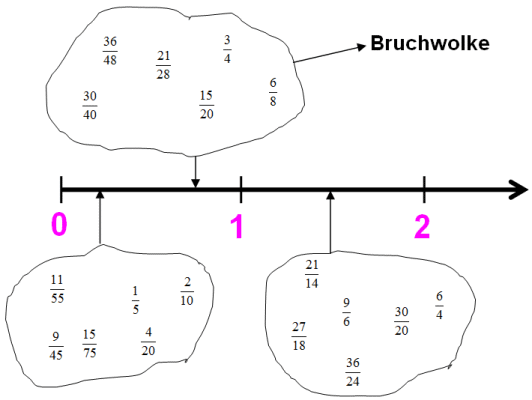
3.1.1 Darstellung
von Brüchen auf dem Zahlenstrahl
|
Merke: |
● Alle Brüche ein- und
derselben Bruchwolke stellen denselben Bruch dar und gehen
durch Kürzen und Erweitern auseinander
hervor.
● Alle Brüche, die denselben
Nenner besitzen heißen gleichnamig.
(3/4 und 10/4 sowie
4/20 und 15/20
und 30/20) |
3.1.2 Erweitern von
Brüchen
|
Merke: |
Man erweitert
einen Bruch, indem man Zähler und Nenner mit derselben (von Null
verschiedenen) Zahl multipliziert. |
Aufgaben:
|
Erweitere den Bruch 4/5
mit 3!
Lösung:
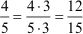 |
Erweitere den Bruch 12/7
mit 6!
Lösung:
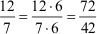
|
Übungsaufgabe:
Erweitere
folgende Brüche nacheinander mit 5; 7 und 10 (im Kopf)!
3/5, 5/6,
4/7, 7/8, 9/10,
5/11 und 0/5
3.1.3 größter gemeinsamer Teiler (g. g. T.)
|
Merke: |
·
Eine natürliche (von Null
verschiedene) Zahl, die eine andere natürliche Zahl ganzzahlig teilt,
heißt Teiler dieser natürlichen Zahl.
·
Jede natürliche Zahl hat
stets sich selbst und die Zahl 1 als Teiler. |
Aufgaben:
Ermittle den größten gemeinsamen Teiler (g. g. T.) der
Zahlen 12 und 18!
|
12 |
1 |
2 |
3 |
4 |
6 |
12 |
|
18 |
1 |
2 |
3 |
6 |
9 |
18 |
→ ggT = 3
Ermittle den größten gemeinsamen Teiler (g. g. T.) der
Zahlen 24 und 48!
|
24 |
1 |
2 |
3 |
4 |
6 |
8 |
12 |
|
24 |
|
|
48 |
1 |
2 |
3 |
4 |
6 |
8 |
12 |
16 |
24 |
48 |
→ ggT = 24
Ermittle den größten gemeinsamen Teiler (g. g. T.) der
Zahlen 8, 16, 24 und 36!
|
8 |
1 |
2 |
|
4 |
|
8 |
|
|
|
|
|
|
|
16 |
1 |
2 |
|
4 |
|
8 |
|
|
16 |
|
|
|
|
24 |
1 |
2 |
3 |
4 |
6 |
8 |
|
12 |
|
|
24 |
|
|
36 |
1 |
2 |
3 |
4 |
6 |
|
9 |
12 |
|
18 |
|
36 |
→ ggT = 4
Übungsaufgaben:
Bestimme von den folgenden Zahlen jeweils das g. g. T.!
|
a) 8 und 10 |
d) 24 und 40 |
|
b) 5 und 25 |
e) 12, 20 und 32 |
|
c) 30 und 45 |
f) 40, 48 und 72 |
Lösungen
3.1.4 Zehnerbrüche
|
Merke: |
Zehnerbrüche sind
Brüche mit dem Nenner 10 oder 100 oder 1000 oder 10000 oder …
Beispiele:
4/10 27/1000
308/10000 15/100
23/10 |
Aufgaben: Schreibe als Zehnerbruch!
Beachte dabei die Stellenwerte!
a) 0,78
= 78/100
b) 0,9
= 9/10
c) 0,456
= 456/1000
d) 1,3
= 13/10
e) 0,07
= 7/100
f) 0,003
= 3/1000
Übungsaufgaben:
1. Schreibe folgende Dezimalbrüche als Zehnerbrüche!
Beachte dabei die Stellenwerte!
a) 0,35 =
b) 0,7 =
c) 0,08 =
d) 0,356 =
e) 1,9 =
f) 0,009 =
g) 25,6 =
2. Schreibe folgende (gemeinen) Brüche als
Dezimalbrüche!
Verwende dazu gegebenenfalls den Taschenrechner!
a) 1/2 =
b) 1/4 =
c) 1/3 =
d) 1/5 =
e) 5/6 =
f) 5/8 =
g) 28/5 =
Lösungen
3.1.5 Kürzen von Brüchen
|
Merke: |
Man kürzt
einen Bruch, indem man Zähler und Nenner durch dieselbe (von Null
verschiedenen) Zahl (Teiler) dividiert. |
Beispiel: Kürze den Bruch 16/24
mit 2!
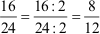
Aufgabe:
Kürze den Bruch 36/48 vollständig!
|
36/48 |
= |
18/24 |
= |
9/12 |
= |
3/4 |
|
|
(mit 2) |
|
(mit 2) |
|
(mit 3) |
|
oder kürzer (mit dem g.g.T.):
|
Merke: |
Ein Bruch heißt
vollständig gekürzt, wenn der größte gemeinsame Teiler (g.g.T.)
von Zähler und Nenner nur noch 1 beträgt (ggT = 1). |
Beispiel: Kürze den Bruch 12/18
vollständig! Bestimme dazu den g.g.T. (größter gemeinsamer Teiler)!
|
12 |
1 |
2 |
3 |
4 |
6 |
|
12 |
|
|
18 |
1 |
2 |
3 |
|
6 |
9 |
|
18 |
→ ggT = 6
|
12 |
= |
12 : 6 |
= |
2 |
|
18 |
|
18 : 6 |
|
3 |
Übung:
Kürze folgende Brüche vollständig!
30/45 ; 75/30 ;
105/45 ; 27/36 ; 18/48
; 18/36 ; 180/150 ; 180/324
Lösung
3.1.6 Gleichnamigmachen von Brüchen
Aufgabe:
Vergleiche das folgende Paar von Brüchen miteinander:
4/6 und 21/28!
|
Merke: |
Um zwei Brüche
miteinander vergleichen zu können, müssen diese gleichnamig
gemacht werden, d. h. sie müssen denselben Nenner (Hauptnenner)
besitzen. |
Lösung:
Gleichnamigmachen der Brüche 4/6 und
21/28!
Vorgehen: Ermittlung des
Hauptnenners (kleinstes gemeinsames Vielfaches der einzelnen Nenner)
|
Merke: |
Um zwei Brüche
gleichnamig zu machen, ermittelt man jeweils gemeinsame Vielfache der
Nenner. Das kleinste gemeinsame Vielfache (k.g.V.) dieser
Nenner wird dann als gemeinsamer Nenner (Hauptnenner)
verwendet. |
1. Ermittlung des k.g.V. durch Vergleich
der Vielfachen der beiden Zahlen:
|
6 |
6 |
12 |
18 |
24 |
|
30 |
36 |
42 |
48 |
54 |
|
60 |
66 |
72 |
78 |
84 |
|
14 |
|
28 |
|
|
|
|
28 |
|
|
|
|
|
56 |
|
|
|
|
84 |
|
3 |
|
k. g. V. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
84 |
|
Ef |
→ k.g.V. = 84 →
Hauptnenner (HN)
= 84
Bestimmung der Erweiterungsfaktoren:
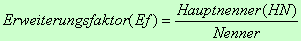 |
→ Ef1 = 84/28
= 3 |
| |
→ Ef2 = 84/6 =
14 |
2. Erweitern der beiden Brüche
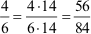

3. Vergleich der beiden Brüche!
|
Merke: |
Man vergleicht zwei
gleichnamige Brüche miteinander, indem man nur die Zähler vergleicht. |
→ 56/84
< 63/84, denn 56 < 63
Andere Variante:
Aufgabe:
Vergleiche das folgende Paar von Brüchen miteinander:
4/20 und 9/45!
Ermittlung des Hauptnenners durch Zerlegung der einzelnen
Nenner in ein Produkt aus Primzahlteilern (Primfaktoren):
|
20 |
2 |
2 |
|
|
5 |
|
|
9 |
|
45 |
|
|
3 |
3 |
5 |
|
|
4 |
|
HN |
2 |
2 |
3 |
3 |
5 |
= |
180 |
Ef |
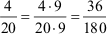
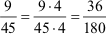
→ 36/180
= 36/180, denn 36 = 36
3.1.7 Übung
zur Ermittlung des Hauptnenners von Brüchen
|
Aufgabe 1: |
Bestimme den Hauptnenner der
folgenden Brüche durch Primfaktorenzerlegung:
¾ ; 7/8 und 1/6
Ermittle zusätzlich die jeweiligen Erweiterungsfaktoren (Ef)! |
Lösung:
|
4 |
2 |
2 |
|
|
|
6 |
|
8 |
2 |
2 |
2 |
|
|
3 |
|
6 |
2 |
|
|
3 |
|
4 |
|
HN |
2 |
2 |
2 |
3 |
= 24 |
Ef |
→ HN = 24
|
Aufgabe 2: |
Bestimme den Hauptnenner der
folgenden Brüche durch Primfaktorenzerlegung:
4/5; 5/6 ;
5/8 ; 7/10 und 1/12!
Ermittle zusätzlich die jeweiligen Erweiterungsfaktoren (Ef)! |
Lösung:
|
5 |
|
|
|
|
5 |
|
24 |
|
6 |
2 |
|
|
3 |
|
|
20 |
|
8 |
2 |
2 |
2 |
|
|
|
15 |
|
10 |
2 |
|
|
|
5 |
|
12 |
|
12 |
2 |
2 |
|
3 |
|
|
10 |
|
HN |
2 |
2 |
2 |
3 |
5 |
=
120 |
Ef |
→ HN = 120
|
Aufgabe 3: |
Bestimme den Hauptnenner der
folgenden Brüche durch Primfaktorenzerlegung:
1/12; 1/6 ;
1/16 und 1/8!
Ermittle zusätzlich die jeweiligen Erweiterungsfaktoren (Ef)! |
Lösung:
|
12 |
2 |
2 |
|
|
3 |
|
4 |
|
6 |
2 |
|
|
|
3 |
|
8 |
|
16 |
2 |
2 |
2 |
2 |
|
|
3 |
|
8 |
2 |
2 |
2 |
|
|
|
6 |
|
HN |
2 |
2 |
2 |
2 |
3 |
=
48
|
Ef |
→ HN = 48
3.1.8 Addition
und Subtraktion von Brüchen
|
Aufgabe 1: |
Addiere die Brüche ½ ; 2/9
und 5/6! Kürze das Ergebnis vollständig! |
|
Merke: |
Man addiert
(subtrahiert) Brüche,
indem man den Hauptnenner ermittelt, sie erweitert und dann nur die Zähler
addiert (subtrahiert). Der gemeinsame Nenner (Hauptnenner) wird beibehalten. |
Lösung:
|
1. |
Hauptnenner ermitteln →
Erweiterungsfaktoren bestimmen (Ef = HN/N) |
kleinstes gemeinsames Vielfache (k.g.V.):
|
2 |
2 |
4 |
6 |
8 |
|
10 |
12 |
14 |
16 |
18 |
20 |
22 |
24 |
26 |
28 |
9 |
|
9 |
|
|
|
|
9 |
|
|
|
|
18 |
|
|
|
|
|
2 |
|
6 |
|
|
6 |
|
|
|
12 |
|
|
18 |
|
|
24 |
|
|
3 |
|
kgV |
|
|
|
|
|
|
|
|
|
18 |
|
|
|
|
|
Ef |
Ef = HN/N
→ k.g.V. = HN = 18
2. Brüche mit den Erweiterungsfaktoren
erweitern und addieren
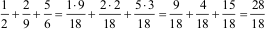
3. Vollständig kürzen
28/18
= 14/9 (Ergebnis)
(mit 2)
|
Aufgabe 2: |
Subtrahiere die Brüche 5/6
und 6/8 voneinander! Kürze das Ergebnis
vollständig! |
Primfaktorenzerlegung:
|
6 |
2 |
|
|
3 |
|
4 |
|
8 |
2 |
2 |
2 |
|
|
3 |
|
HN |
2 |
2 |
2 |
3 |
= 24 |
Ef |
→ HN = 24

2/24
= 1/12 (Ergebnis)
(mit 2)
3.1.9
Übungsaufgaben zur Addition und Subtraktion von Brüchen
|
1. |
Addiere folgende
Brüche! Kürze die Ergebnisse vollständig! |
|
|
a) |
1/3 + 1/3 = |
i) |
3/4
+ 5/8 + 1/6 = |
|
|
b) |
2/5 + 1/5 =
|
k) |
3/5 + 5/7 + 1/2 = |
|
|
c) |
3/8 + 5/8 = |
l) |
4/5 + 5/6 + 3/8 = |
|
|
d) |
3/4 +
2/4 +
1/4 = |
m) |
5/12 + 7/16 = |
|
|
e) |
1/4
+ 1/2= |
n) |
3/15 + 11/30 = |
|
|
f) |
2/3
+ 3/4 = |
o) |
8/9 + 5/6 + 1/2 +
13/18 = |
|
|
g) |
2/3 + 4/5 = |
p) |
3/4 + 5/6
+ 7/8 + 5/12 + 4/9 + 7/15 = |
|
|
h) |
3/4
+ 1/2 + 1/4 = |
q) |
5/30 +
11/15 + 7/45 + 3/10 = |
|
2. |
Subtrahiere
folgende Brüche! Kürze die Ergebnisse vollständig! |
|
|
a) |
2/3
– 1/3 = |
e) |
45/8
- 11/8 = |
|
|
b) |
4/5
– 2/5 = |
f) |
47/9
- 25/6 = |
|
|
c) |
4/5
– 1/2 = |
g) |
125/8
– 73/5 = |
|
|
d) |
7/8
– 3/4 = |
h) |
82/3
– 45/7 = |
|
3. |
Von einem
Stoffballen, der 62 m misst, werden nacheinander folgende Mengen
verkauft: 33/4 m, 71/2 m, 22/5
m, 14/5 m, 63/4 m, 103/10
m und 121/2 m.
Wie groß (in Metern) ist der Restbestand an Stoff? |
|
4. |
Addiere: 23 cm +
1/4 m 14,5 cm + 3/8 m +1,75
m +21/4 m 113/4 m! |
3.2 Multiplizieren und
Dividieren von Brüchen
3.2.1 Multiplikation
von Brüchen
|
Merke: |
Man multipliziert
zwei Brüche miteinander, indem man sowohl die beiden Zähler als auch die
beiden Nenner miteinander multipliziert.
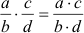
Es ist sinnvoll, die
Brüche vor dem Multiplizieren zu kürzen, auch "über Kreuz". |
Beispiele:
a)
|
9 |
* |
28 |
= |
9 *
28
|
= |
1 *
2 |
= |
1 * 1 |
= |
1 |
|
14 |
36 |
14
* 36
|
1
* 4 |
1 * 2 |
2 |
b)
|
12 |
* |
15 |
* |
5 |
= |
12
* 15 * 5
|
= |
1
* 3 *
5 |
= |
1 * 1 * 1 |
= |
1 |
|
25 |
24 |
6 |
25
* 24
* 6
|
5
* 2 * 6
|
1 * 2 * 2 |
4 |
Übungsaufgaben:
Lösungen
3.2.2 Division von
Brüchen
|
Merke: |
Man dividiert zwei
Brüche durcheinander, indem man den ersten Bruch mit dem Kehrwert
(Reziprokes) des zweiten Bruches multipliziert.

Die Brüche können
nur bei der Multiplikation gekürzt werden! |
Beispiele:
a)
|
3 |
: |
9 |
= |
3 |
* |
10 |
= |
3 *
10
|
= |
1 * 2 |
= |
2 |
|
5 |
10 |
5 |
9 |
5
* 9
|
1
* 3 |
3 |
b)
|
25 |
: |
35 |
= |
25 |
* |
36 |
= |
25
* 36
|
= |
5
* 3 |
= |
15 |
|
48 |
36 |
48 |
35 |
48 *
35
|
4 * 7 |
28 |
Übungsaufgaben:
Lösungen
|