|
Lineare
Funktionen
[Begriff
der linearen Funktion] [lineare
Funktion der Form y = mx + n]
1
Begriff
der linearen Funktion
1. 1
Aufgabe:
Gegeben sei eine Abbildung F mit
folgender Zuordnungsvorschrift:
→ Jeder natürlichen Zahl x wird ihre Hälfte y zugeordnet.
a) Gib in einer
Zuordnungstabelle mindestens 5 Zahlenpaare an, die dieser Abbildung genügen!
b) Stelle die gegebene Abbildung grafisch dar!
Lösung:
|
a) Zuordnungstabelle:
|
x |
y = 1/2*x |
|
0 |
0 |
|
1 |
1/2 |
|
2 |
1 |
|
3 |
3/2 |
|
4 |
2 |
|
5 |
5/2 |
|
6 |
3 |
|
7 |
7/2 |
|
8 |
4 |
x  N
N
y  Q+
Q+ |
b) grafische Darstellung:
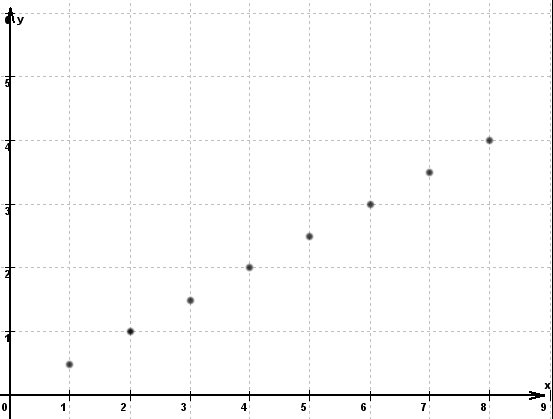 |
 Jede eindeutige Abbildung heißt Funktion.
Jede eindeutige Abbildung heißt Funktion.
1.2
Begriffe:
| Originalmenge X |
 |
Definitionsbereich X der Funktion |
| Bildmenge Y |
 |
Wertebereich (Wertevorrat) Y der Funktion |
| Element der Originalmenge x |
 |
Argument x (x  X)
X) |
| Element der Bildmenge y |
 |
Funktionswert y (y  Y)
Y)
(y ist der zu x gehörige Funktionswert) |
| Schreibweise |
 |
y = f(x) ..... y ist eine Funktion von x |
| Zuordnungsvorschrift y = 1/2*x |
 |
Funktionsgleichung y = f(x) = 1/2*x |
1. 3
Beschreibungsmöglichkeiten einer Funktion:
(1) Wertetabelle
y = 2x |
(2) geordnete Zahlenpaare
[x; y] |
(3) grafische Darstellung
y = f(x) = 2x |
|
x |
y = 2x |
|
-1 |
-2 |
|
0 |
0 |
|
1 |
2 |
|
2 |
4 |
|
3 |
6 |
|
[-1; -2][0; 0]
[1; 2]
[2; 4]
[3; 6] |
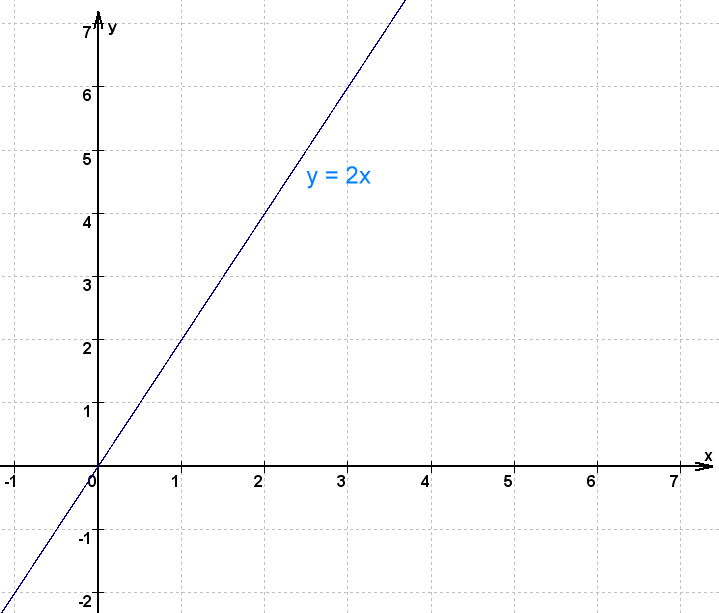 |
 Eine Funktion heißt linear,
wenn das Bild der grafischen Darstellung
Eine Funktion heißt linear,
wenn das Bild der grafischen Darstellung
eine Gerade
ist.
--------------
2 Einfache
lineare Funktionen der Form
y = mx + n
2. 1 Erklärung der Variablen in der
Funktionsgleichung y = mx + n
y
→ Ordinate (y-Wert) [y
Î R]
x
→ Abszisse (x-Wert) [x Î
R]
m
→ Anstieg der Gerade (Funktionsbild; Graph) [m
Î R]
n
→ Ordinate des Schnittpunktes der Gerade mit der y-Achse [n
Î R]
2. 2 Graphische Darstellung der linearen Funktion
| (1) y = 3x - 4
Wertetabelle:
|
Y = 3x - 4 |
x |
|
2 |
2 |
|
-1 |
1 |
|
-4 |
0 |
|
-7 |
-1 |
|
-10 |
-2 |
Grafische Darstellung:
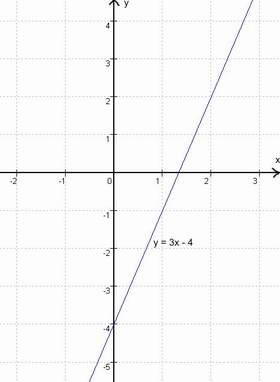
|
(2) y = -1/2x + 3
Wertetabelle:
|
Y = -1/2x + 3 |
x |
|
0 |
6 |
|
1 |
4 |
|
2 |
2 |
|
3 |
0 |
|
4 |
-2 |
Grafische Darstellung:
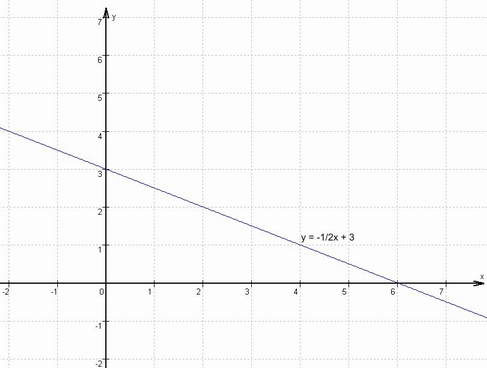
|
2. 3 Monotonieverhalten
m < 0 →
Der Graph der linearen Funktion ist im gesamten Definitionsbereich (-
¥ £ x
£ ¥) monoton fallend.
m > 0 →
Der Graph der linearen Funktion ist im gesamten Definitionsbereich (-
¥ £ x
£ ¥) monoton steigend.
2. 4 Nullstellen
Die Nullstelle einer linearen Funktion ist die Abszisse des Schnittpunktes
des Graphen mit der x-Achse.
Beispiel:
y = -1/2x + 3
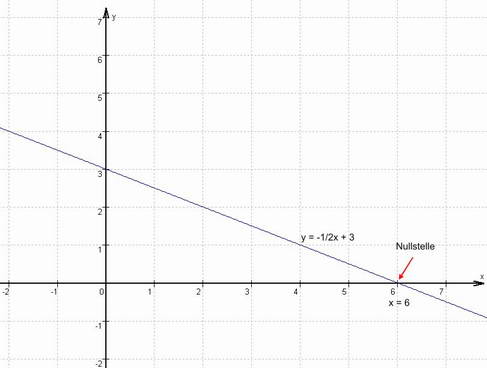
2. 5 Berechnung der Nullstelle
Gedanke: Die Ordinate der Nullstelle ist stets Null.
→ Y = 0
→ 0 = -1/2x + 3
(→ Gleichung nach x umformen!)
→ -3 = -1/2x
→
6 = xo →
Die Nullstelle der linearen Funktion y = -1/2x + 3 lautet
xo = 6.
|