|
TERME und
TERMUMFORMUNGEN
1. Begriffe
| Begriff |
Beschreibung |
Beispiele |
| Terme |
Ziffern, Variable und Zusammensetzungen aus ihnen mit
Hilfe der Rechenzeichen |
3 ; a ;
3/4 ; 2,7 + x ; (6 -
4a) - 8b ;
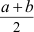 ; ;
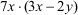 |
| Gleichungen |
Ausdrücke, in denen zwei Terme durch ein
Gleichheitszeichen verbunden sind |
5 + 7 = 12 ; 4 + x = 5,5 ;
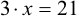 |
| Ungleichungen |
Ausdrücke, in denen zwei Terme durch < bzw. durch
> verbunden sind |
5 + 3 < 12 ; 12 - y > 20 ;
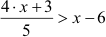 |
2.
Einfache Termumformungen
|
Merke: |
Alle Termumformungen
führen zu einander äquivalenten Termen. |
Aufgabe:
Vereinfache den Term 3x + 4y -5x
-3y -6x + 2y!
|
Vorgehen: |
Fasse
nur Ausdrücke mit den gleichen
Variablen zusammen! |
Lösung:
|
3x + 4y -5x -3y -6x + 2y |
= 3x - 5x - 6x +4y -3y +2y |
Ordnen! |
| |
= -8x + 3y |
Zusammenfassen! |
3.
Addition und Subtraktion von
Summentermen
a) Addition
| Gegeben: |
T1 = 4x - 7y |
|
| |
T2 = -9x + 4y |
|
| Bilde und vereinfache T1 + T2! |
|
|
| |
|
|
| Lösung: |
(4x - 7y) + (-9x + 4y) |
Klammern auflösen! |
| |
= 4x - 7y - 9x + 4y |
Ordnen! |
| |
= 4x - 9x - 7y + 4y |
Zusammenfassen! |
| |
= -5x -3y |
Ergebnis |
| |
|
|
|
Auflösen der Klammern: |
a +
(b - c) = a + b - c
Steht ein Plus vor der Klammer, kann die Klammer einfach
weggelassen werden.
Die Vor- bzw. Rechenzeichen des zweiten Summanden bleiben erhalten. |
a) Subtraktion
| Gegeben: |
T1 = 8a + 2b |
|
| |
T2 = -7b + 5a |
|
| Bilde und vereinfache T1 - T2! |
|
|
| |
|
|
| Lösung: |
(8a + 2b) - (-7b + 5a) |
Klammern auflösen! |
| |
= 8a + 2b + 7b - 5a |
Ordnen! |
| |
= 8a -5a + 2b + 7b |
Zusammenfassen! |
| |
= 3a + 9b |
Ergebnis |
| |
|
|
|
Auflösen der Klammern: |
a -
(b - c) = a - b + c
Steht ein Minus vor der Klammer, kann die Klammer
weggelassen werden, wenn sich die Vorzeichen ändern.
Die Vor- bzw. Rechenzeichen des Subtrahenden ändern sich
entgegengesetzt! |
Beispielaufgaben:
| 1. |
Schreibe den folgenden
Term nur mit positiven (+) Rechenzeichen! |
| |
6x - 23y -7z |
→ |
6x
+ (-23y) + (-7z) |
| |
|
|
|
| 2. |
Schreibe den
folgenden Term nur mit negativen (-) Vorzeichen! |
| |
12x - 8y +9z |
→ |
+ (-12x)
+ (-8y) + (-9z) |
| |
|
|
|
| 3. |
Schreibe den
folgenden Term nur mit negativen (-) Rechenzeichen! |
| |
1,3a + 9,7b + 4,5c |
→ |
-
(+1,3a) - (-9,7b)
- (-4,5c) |
| |
|
|
|
| 4. |
Löse die
Klammern auf und fasse zusammen! |
| |
26x - (12x
-34) + (-23 + 20x) - (-8x +10) |
| |
= 26x - 12x +
34 - 23 + 20x + 8x - 10 |
| |
= 26x - 12x +
20x + 8x + 34 -23 -10 |
| |
=
42x + 1 |
4. Umformung eines Produktterms in einen Summenterm und umgekehrt
Anwendung des Distributivgesetzes:
(1) Umformen eines Produktterms in einen Summenterm
(Ausmultiplizieren)
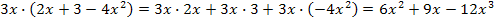
|
Hinweis: |
Multipliziere den Faktor
3x mit jedem Summanden in der Klammer und
addiere die so entstandenen Produkte! |
Beispiele:
| a) -4y(x - 3x² + 1,5) |
=
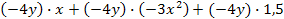 |
| |
= -4xy + 12x²y - 6y |
| |
= 12x²y - 4xy - 6y |
b)
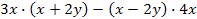 |
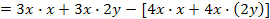 |
| |
= 3x² + 6xy - [4x² - 8xy] |
| |
= 3x² + 6xy - 4x² + 8xy |
| |
= -x² + 14xy |
(2) Umformen eines Summenterms in einen Produktterm
(Ausklammern oder Faktorisieren)
|
Vorgehen: |
1. |
Suche in jedem Summanden
einen (den) gemeinsamen Faktor! |
| |
2. |
Klammere diesen
gemeinsamen Faktor aus!
(Schreibe den Faktor vor eine Klammer!) |
| |
3. |
Bilde die Restsumme, indem du jeden Summanden in der
Klammer durch diesen ausgeklammerten Faktor dividierst!
Kürze und addiere die so entstandenen Quotienten! |
| |
4. |
Multipliziere den ausgeklammerten Faktor mit der
Restsumme! |
Beispiele:
| a) 6x² - 2x |
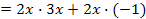 |
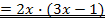 |
| b) -3ax - 12xy + 15x² |
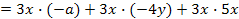 |
|
| |
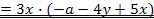 |
|
| c) 12a² - 9a + 27 |
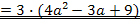 |
|
5.
Multiplikation von Summentermen
(a + b)(c + d) = ac + ad + bc + bd
Man
multipliziert jeden Summanden der einen Klammer mit jedem Summanden der
zweiten Klammer und addiert die so entstandenen Produkte.
Gleiche Variablenausdrücke fasst man zusammen.
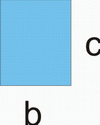
Diese Regel kann für a, b, c, d durch Rechteckflächen veranschaulicht werden:
 |
 |
 |
 |
 |
 |
|
(a + b)(c + d) |
= |
ac |
+ ad |
+ bc |
+ bd |
Beispiele:
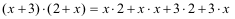 =
2x + x² + 6 + 3x = x² +5x +6 =
2x + x² + 6 + 3x = x² +5x +6
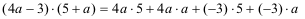 =
20a + 4a² - 15 - 3a = 4a² + 17a - 15 =
20a + 4a² - 15 - 3a = 4a² + 17a - 15
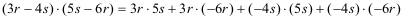 = 15rs
- 18r² - 20s² + 24rs = 15rs
- 18r² - 20s² + 24rs
= -18r² + 39rs - 20s²
Kürzer:
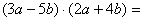 6a² +
12ab - 10ab - 20b² = 6a² + 2ab 20b² 6a² +
12ab - 10ab - 20b² = 6a² + 2ab 20b²
Übungsaufgaben - st01:
Multiplizieren Sie die Terme und fassen Sie gleiche Variablenausdrücke
zusammen!
(1) 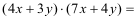
(2) 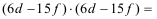
(3) 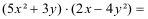
(4) 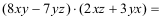
(5) 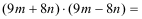
(6) 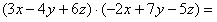
Lösungen
6. Die „Binomischen Formeln“ als Spezialfälle der Multiplikation von
Summentermen
|
(a + b)(a + b ) = (a + b)² = a² + 2ab + b²
(a - b)(a - b) = (a - b)² = a² - 2ab + b²
(a + b)(a – b) = a² - b²
|
|
Mit Hilfe der binomischen Formeln lassen sich in
besonderen Fällen Summen in Produkte umformen.
Summen, die sich in die Form (a + b)² bringen lassen,
bezeichnet man als
vollständige Quadrate.
|
Beispiele:
Schreiben Sie folgende Produkte (Potenzen) mit Hilfe der binomischen Formeln als
Summen!
T1
= (y + 4)² = y² + 2·y·4 + 4² = y² + 8y + 16
T2 = (p – 3)² = p² - 2·p·3 + 3² = p²
- 6p + 9
T3 = (7w + 5z)(7w – 5z) = (7w)² - (5z)² =
49w² - 25z²
Schreiben Sie die folgenden Summen mit Hilfe der binomischen Formeln als
Produkte (vollständige Quadrate)!
T1
= x² + 6x + 9 = x² + 2·x·3 + 3² = (x + 3)(x + 3) =
(x + 3)²
T2 = 16r² - 56rs + 49s² = (4r)² - 2·28·rs + (7s)² = (4r – 7s)(4r –
7s) = (4r – 7s)²
T3 = 81x² - 64y² = (9x – 8y)²
↓
Im
Allgemeinen lassen sich beliebige Terme nicht komplett zu einem
vollständigen Quadrat umformen. Mit Hilfe der
„Quadratischen Ergänzung“
lassen sich diese Terme aber derart umformen, dass diese ein vollständiges
Quadrat enthalten.
|
Eine "quadratische Ergänzung" macht einen
Term der Form x² + p zu einem vollständigen Quadrat der Form (x + p)²
|
Beispiel:
(1)
T1 = x² - 10x
↓
quadratische Ergänzung zu (x² - 8x) bestimmen
= x² - 10x + (5² -
5²)
→ Man ermittelt die "quadratische
Ergänzung",
indem man das Quadrat von p/2 bildet!
↓umformen
→ Damit
man die "quadratische Ergänzung" dem
Term bedenkenlos hinzufügen kann, muss man
sie gleichzeitig wieder
subtrahieren! Hier: (5² - 5²)
= (x² - 10x + 5²) - 25
↓
vollständiges
Quadrat mit Hilfe der binomischen
Formel angeben
=
(x - 5)²
- 25
7.
Der arithmetischer
Beweis (Beweisführung von Sätzen)
Wie ist ein Beweis aufgebaut?
|
Voraussetzung: |
Was wird vorausgesetzt? |
|
Behauptung: |
Was wird behauptet? |
| Beweis: |
Beweis der Behauptung mit Hilfe der Voraussetzung
sowie anderen schon bewiesenen Sätzen, Definitionen bzw. Regeln |
Beispiele:
| 1. |
Die Summe von vier aufeinanderfolgenden natürlichen
Zahlen ist stets gerade. |
|
Voraussetzung: |
n; n+1; n+2; n+3; n
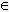 N N |
|
Behauptung: |
2/n+(n+1)+(n+2)+(n+3)
(2/n → 2 ist ein
Teiler von n) |
| Beweis: |
2/n+(n+1)+(n+2)+(n+3)
= 2/n+n+1+n+2+n+3
= 2/4n+6
= 2/2(2n+3) →
2 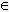 N
N
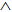 (2n+3)
(2n+3)
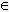 N N
→ 2/2
→ (Regel zur Teilbarkeit von Produkten)
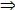 2/2(2n+3) 2/2(2n+3)
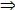 2/4n+6 2/4n+6
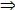 2/n+n+1+n+2+n+3 2/n+n+1+n+2+n+3
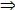 2/n+(n+1)+(n+2)+(n+3)
w. z. b. w. 2/n+(n+1)+(n+2)+(n+3)
w. z. b. w.
|
| 2. |
Die Summe von drei aufeinanderfolgenden
ungeraden, natürlichen Zahlen ist stets ungerade. |
|
Voraussetzung: |
2 n+1; 2n+3; 2n+5; n
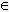 N N |
|
Behauptung: |
(2n+1)+(2n+3)+(2n+5)
→ ungerade, d. h. nicht durch 2 teilbar |
|
Beweis: |
2n+1+2n+3+2n+5
= 6n+9
= 2(3n+9/2) →
2 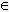 N
N
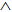 (3n+9/2)
(3n+9/2)
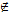 N N
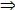 2 2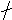 (3n+9/2)
(3n+9/2)
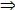 2 2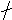 6n+9
6n+9
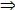 2 2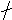 2n+1+2n+3+2n+5
2n+1+2n+3+2n+5
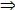 2 2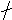 (2n+1)+(2n+3)+(2n+5)
w. z. b. w.
(2n+1)+(2n+3)+(2n+5)
w. z. b. w.
|
| 3. |
Wenn die kleinste von drei
aufeinanderfolgenden natürlichen Zahlen ungerade ist, so ist deren Summe
durch 6 teilbar. |
|
Voraussetzung: |
2 n+1; 2n+2; 2n+3; n
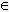 N N |
|
Behauptung: |
6/(2n+1)+(2n+2)+(2n+3) |
Beweis:
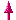 |
(2n+1)+(2n+2)+(2n+3)
= 2n+1+2n+2+2n+3
= 6n+6
= 6(n+1) → 1 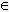 N
N
→
6/6
→ (Regel zur Teilbarkeit von Produkten)
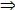 6/6(n+1)
6/6(n+1)
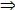 6/6n+6 6/6n+6
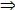 6/2n+1+2n+2+2n+3 6/2n+1+2n+2+2n+3
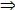 6/(2n+1)+(2n+2)+(2n+3)
w. z. b. w. 6/(2n+1)+(2n+2)+(2n+3)
w. z. b. w.
|
|

