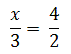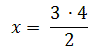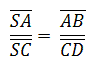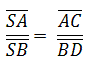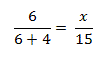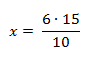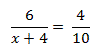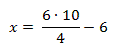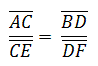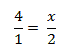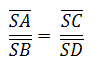|
Ähnlichkeit
1.
Maßstäbliche
Vergrößerungen und Verkleinerungen
|

Original der BR 218 |

 |

HO-Modell der BR 218 |
Für eine maßstäbliche Vergrößerungen und
Verkleinerungen ist die Angabe eines Abbildungsmaßstabes notwendig.
------------
Beim HO-Modell der BR 218 beträgt der Abbildungsmaßstab
1 : 87, d. h. 1 cm beim HO-Modell entsprechen 87 cm beim
Original.
oder
anders ausgedrückt: Das Original ist
87 x größer als das HO-Modell.
→ Allgemein: Das Original
ist k-mal größer als das Modell.
(k ist dabei der Vergrößerungsfaktor)
Beispiele für maßstäbliche
Vergrößerungen und Verkleinerungen
(1) Ein D-Zug-Wagen hat im Original
eine Länge von 21,75 m.
Wie lang ist dieser Wagen bei einem H0-Model
(Abbildungsmaßstab 1 : 87)?
Lösung:
gegeben: Wagenlänge
Original = 21,75 m = 2175 cm
Abbildungsmaßstab = 1 : 87
gesucht: Wagenlänge
Modell (in cm)
Lösung: 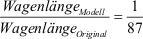
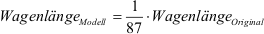
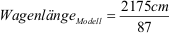
Wagenlänge Modell =
25 cm
(2) Auf einer Landkarte im Maßstab von
1 : 50000 beträgt die Entfernung zweier Orte 2,5 cm.
Wie weit sind die beiden Orte in Wirklichkeit (in der
Natur) von einander entfernt?
Lösung:
gegeben: Kartenmaßstab 1 :
50000
Entfernung Karte = 2,5
cm
gesucht: Entfernung
Natur (in km)
Lösung: 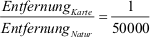
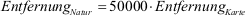
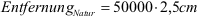
Entfernung Natur =
125000 cm = 1,25 km
2.
Zentrische Streckungen
Definition:
Eine zentrische Streckung der Ebene ist eine eineindeutige
Abbildung der Ebene auf sich, bei der jedem Punkt P der
Ebene sein Bildpunkt P' folgendermaßen zugeordnet wird:
-
Ein Punkt wird als Streckungszentrum
Z festgelegt.
-
Eine positive reelle Zahl wird als
Streckungsfaktor k festgelegt.
-
P' liegt auf dem Strahl ZP' (ZP' = k *
ZP)
→ k = ZP'/ZP
-
Z
hat sich selbst als Bildpunkt.
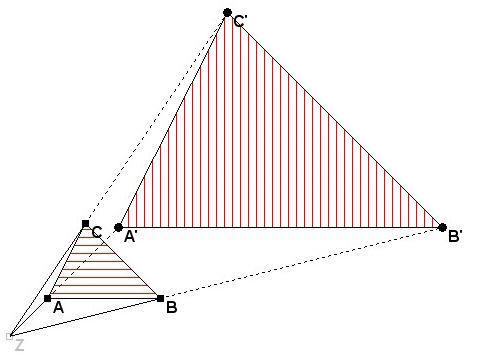
Beispielaufgabe: Das Dreieck ABC soll
zentrisch gestreckt werden.
a) Zeichnen Sie in ein Koordinatensystem das Dreieck A(5;1),
B(6;5) und C(4;4)!
b) Zeichnen Sie nun das Dreieck A'B'C', das bei einer
zentrischen Streckung des Dreiecks ABC mit dem
Streckungszentrum
Z(2;1) und dem Streckungsfaktor k = 5/3 entsteht! Hinweise
zur Lösung: k = ZA'/ZA = ZB'/ZB = ZC'/ZC = A'B'/AB = A'C'/AC
= B'C'/BC = 5/3 (ZA = 3 Einheiten und ZA' = 5 Einheiten) Zur
Konstruktion dieser zentrischen Streckung benötigen Sie die
konstruktive Vervielfältigung einer Strecke!
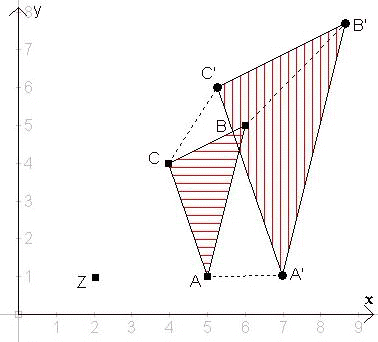
Übungsaufgabe 1: Das Dreieck
ABC soll zentrisch gestreckt werden.
a) Zeichnen Sie in ein Koordinatensystem das Dreieck A(5;1),
B(6;5) und C(4;4)!
b) Zeichnen Sie nun das Dreieck A'B'C', das bei einer
zentrischen Streckung des Dreiecks ABC mit dem
Streckungszentrum
Z(2;1) und dem Streckungsfaktor k = 3 entsteht!
Lösung
Übungsaufgabe 2: Das Dreieck
PQR soll zentrisch gestreckt werden.
a) Zeichnen Sie in ein Koordinatensystem das Dreieck P(2;1),
Q(5;1) und R(2;3)!
b) Zeichnen Sie nun das Dreieck P'Q'R', das bei einer
zentrischen Streckung des Dreiecks ABC mit dem
Streckungszentrum Z(0;0) und dem Streckungsfaktor k = 2
entsteht!
c) Berechnen Sie den Flächeninhalt A des Dreiecks PQR!
d) Es sei A' der Flächeninhalt des Dreiecks P'Q'R'.
Geben Sie das Verhältnis A' : A an!
Lösung
|
Merke: |
Ebene
Figuren (z. B. Dreiecke und Vierecke), die durch
zentrische Streckung auseinander hervorgehen, sind
einander ähnlich.
Kreise und Quadrate sind stets einander
ähnlich.
|
3.
Der Strahlensatz
|
1. Teil des Strahlensatzes: |
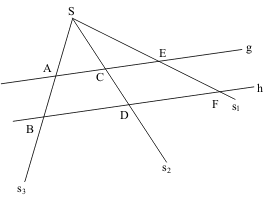
Werden zwei Strahlen mit gemeinsamen Anfangspunkt S von zwei Parallelen geschnitten, dann verhalten sich die
Abschnitte auf dem einen Strahl zueinander wie die
gleichliegenden Abschnitte auf dem anderen.
|
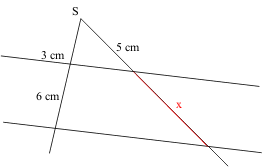
Beispiele:
|
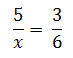 →
→
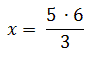 →
x = 10 cm →
x = 10 cm |
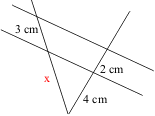 |
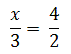 →
→
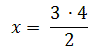 →
x = 6 cm →
x = 6 cm |
|
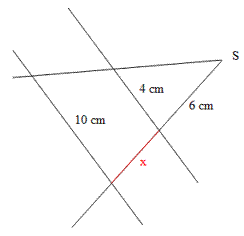
2. Teil des Strahlensatzes: |
Werden zwei Strahlen mit gemeinsamen Anfangspunkt von
zwei Parallelen geschnitten, dann verhalten sich je zwei
Parallelenabschnitte zueinander wie die zugehörigen
Strahlenabschnitte ein und desselben Strahls.
|
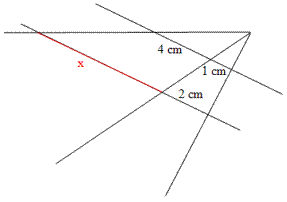
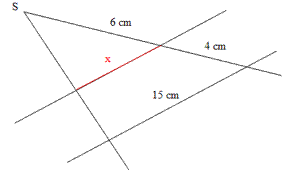
Beispiele:
|
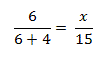 →
→
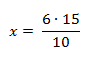 →
x = 9 cm
→
x = 9 cm |
|
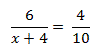 →
→
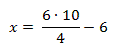 → x = 9 cm
→ x = 9 cm |
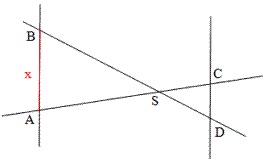
| AS = 6 cm |
SC = 3 cm |
CD = 2 cm |
|
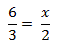 →
→
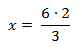 → x = 4 cm
→ x = 4 cm |
|
3. Teil des Strahlensatzes: |
Werden zwei Strahlen mit gemeinsamen Anfangspunkt von
zwei Parallelen geschnitten, dann verhalten sich die
Abschnitte auf der einen Parallelen zueinander wie die
gleichliegenden Abschnitte auf der anderen Parallelen.
|
Beispiel:
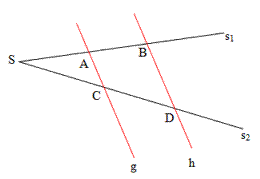
Umkehrung
des 1. Teiles des Strahlensatzes: |
Bilden gleichliegende Strahlenabschnitte zweier Strahlen
mit gemeinsamen Anfangspunkt das gleiche Verhältnis, so
werden sie von parallelen Geraden erzeugt.
 |
Wenn gilt:
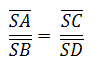
dann folgt daraus:
g
║ h |
|
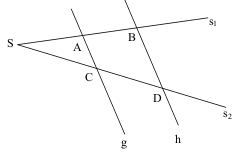
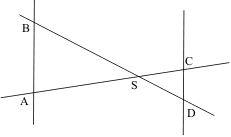
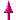 Beispielaufgabe:
|
Problem: |
Landvermessung für eine
Trasse der Autobahn
Die geplante Trasse
(Messstrecke AB) führt durch ein
unübersichtliches Sumpfgebiet, Abstecken und Messung
sind in diesem Gebiet nicht möglich. Aus diesem
Grunde werden auf dem festen Untergrund (Wiese -
Grasland - Weg) Messpunkte eingerichtet.
Vom Standort P (Standort des Beobachters) werden diese
Messpunkte angepeilt.
Aus den Peilungen ergeben sich
folgende Streckenlängen:
PB = 703 m
PD = 120 m
CD = 100 m
|
Lösung des Problems nach
dem 2. Teil des Strahlensatzes:
Nach dem 2. Teil des Strahlensatzes gilt:
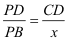
→
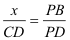 → →
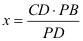 → →
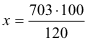 →
x = 585,83 m
→
x ≈ 586 m →
x = 585,83 m
→
x ≈ 586 m
Die Messstrecke durch das
Sumpfgebiet hat eine Länge von rund 586 m.
 |





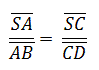
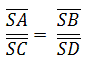

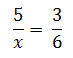
 →
→