|
Die Prozentrechnung
Inhalt:
1.
Einführung |
2.
Beispielaufgaben und Lösungen zu den Größen der Prozentrechnung |
3.
Der vermehrte und der verminderte Grundwert |
4.
Übungsaufgaben zur Prozentrechnung |
|
|
|
|
|
1. Einführung
| |
In einem Sonderverkauf wird auf
verschiedene Artikel ein Preisnachlass gewährt: z. B.:
- ein Hemd im Wert von 25,00 € ein Nachlass von 8,00 €
- ein Pullover im wert von 50,00 € ein Nachlass von 15,00 €
Bei welchem Artikel ist der Preisnachlass bezogen
auf den Wert des Artikels höher? |
Lösung:
Bereitstellung der Lösung mit Hilfsmitteln (Stoff), die schon bekannt sind:
Bruchrechnung
Ergebnis:
Der Preisnachlass beim Hemd ist bezogen auf
den Wert des Artikels größer als beim Pullover.
Problem:
Beim Vergleich von vielen Artikeln ist diese
Methode sehr ungünstig und zeitaufwendig, da man immer wieder einen
gemeinsamen Nenner bestimmen muss.
Ein direkter Vergleich solcher Preisnachlässe ist also auf diese Weise nicht
möglich!

Besser: Einheitliche Vergleichszahl
schaffen!

Die Zahl 100

Also jetzt: Preisnachlass ermitteln
bezogen auf jeweils 100 €


"von
Hundert"
→
lat. "pro centum"
→
%
Schreibweisen:
| 32 % |
"Prozent" |
Alle 3 Schreibweisen werden gleichberechtigt
verwendet! |
| 32 v. H. |
"von Hundert" |
|
0,32 |
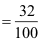 |
Die Größen der Prozentrechnung:
| z. B.: |
8,00 € |
von |
25,00 € |
→ |
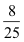 |
= 0,32
= 32 % |
 |
|
 |
|
|
 |
Prozentwert
("Teil vom Ganzen") |
|
Grundwert
("Das Ganze" = 100 %) |
|
|
Prozentsatz
(%) |
Die Grundgleichung der
Prozentrechnung:
|
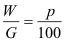 |
|
W...
Prozentwert
G... Grundwert
p... Prozentsatz (in %)
100 ... 100 % |
| |
ð Umformung nach den jeweiligen Größen:
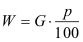 |
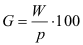 |
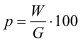 |
| |
|
|
|
Prozentwert |
Grundwert |
Prozentsatz |
2.
Beispielaufgaben zu den 3 Größen der Prozentrechnung
Hinweis:
Die Beispielaufgaben sind bewusst so gewählt, dass man sie zum Vergleich auch im
Kopf lösen könnte!
2. 1. Der Prozentwert
Aufgabe: Wie viel Euro sind 12 % von
500,- €?
Lösungsmöglichkeiten:
| (1) Grundgleichung der Prozentrechnung
→ |
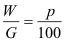 |
W = ?
G = 500 €
p = 12 % |
|
→ |
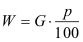
|
|
| |
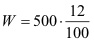 |
|
| |
W = 60 € |
→ 12 % von 500 € sind 60 €. |
|
---------------------------------------------------------------------------- |
| (2) Zurückführung auf 1 Prozent (1 %)
→ |
1 % von 500 € (= 500/100) = 5 € |
|
→ |
12 % von 500 €
(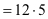 ) =
60 € ) =
60 € |
|
|
---------------------------------------------------------------------------- |
| (3) Proportion - gerades Verhältnis (Dreisatz)
→ |
500 €  100 %
100 %
x
 12 %
12 % |
|
→ |
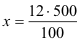 |
| |
x = 60 € |
|
---------------------------------------------------------------------------- |
| (4) einfache und kurze Schreibweise
→ |
12 % (= 12/100) = 0,12 |
| |
12 % von 500 €
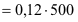 =
60 €
=
60 € |
|
| |
|
2. 2. Der Prozentsatz
Aufgabe: Wie viel Prozent (%) sind 36 m
von 144 m?
Lösungsmöglichkeiten:
| (3) einfache und kurze Schreibweise
→ |
36 m von 144 m
→ Vergleich
→
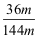 |
= 0,25 |
| |
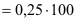 = 25 %
= 25 % |
|
Einfache Prozentsätze:
| 100 % = 1
(Ganzes) 50 % = 0,5 (= 1/2)
75 % = 0,75 (= 3/4)
33,33... % = 0,3333... (= 1/3)
25 % = 0,25 (= 1/4)
20 % = 0,2 = (= 1/5) |
|
231 % = 2,31
116,5 % = 1,165
88,6 % = 0,886
12,45 % = 0,1245
2,5 % = 0,025
0,56 % = 0,0056 |
|
1,85 = 185 %
1 (Ganzes) = 100 %
0,98 = 98 %
0,752 = 75,2 %
0,031 = 3,1 %
0,007 = 0,7 % |
|
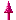
2. 3. Der Grundwert
Aufgabe: Berechne den Grundwert, wenn 9 %
dieses Grundwertes 72 kg sind!
Lösungsmöglichkeiten:
|
---------------------------------------------------------------------------- |
| (2) Proportion - gerades Verhältnis (Dreisatz)
→ |
x
 100
% 100
%
72 kg  9 %
9 % |
|
→ |
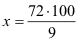 |
| |
x = 800 kg |
2. 4. Einfache Übungen
-
einfache
Prozentsätze (Kopfrechnen)
-
einfache
Prozentwertaufgaben (Kopfrechnen)
-
einfache
Prozentsatzaufgaben (Kopfrechnen)
3.
Der verminderte und der
vermehrte Grundwert
3. 1 Grundlagen
Beim vermehrten Grundwert wird der normale Grundwert (Das
Ganze = 100 %) um einen bestimmten Prozentsatz vermehrt (gesteigert).
Beim verminderten Grundwert wird der normale Grundwert (Das
Ganze = 100 %) um einen bestimmten Prozentsatz vermindert (verringert).
3. 2. Beispielaufgaben
- Der Preis einer Ware, wurde um 12 % erhöht und beträgt
jetzt 135,60 €.
a) Wie viel Euro betrug der Preis vorher?
b) Wie groß ist die Preiserhöhung
Lösung:
a) Ansatz:
135,60 €
 112 %
112 %
x
 100 %
100 % |
→ |
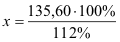 |
→ |
x = 121,07 € |
b) Preiserhöhung: 135,60 € - 121,07 =
14,53 €
(vermehrter Grundwert)
- Der Verkaufspreis für eine Ware beträgt 1205,70 €.
Wie hoch ist der darin enthaltene Mehrwertsteuerbetrag bei einem
derzeitigen Mehrwertsteuersatz von 19 %?
Lösung:
Ansatz:
1205,70 €
 119 %
119 %
x
 19 %
19 % |
→ |
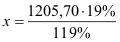 |
→ |
x = 192,51 € |
(vermehrter Grundwert)
- Nach einer Preissenkung um 11½
% beträgt der Preis für eine Ware nur noch 78,75 €.
Wie hoch war der Preis vor der Senkung?
Lösung:
Ansatz:
78,75 €
 88,5 %
88,5 %
x
 100 %
100 % |
→ |
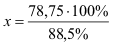 |
→ |
x = 88,98 € |
(verminderter Grundwert)
-
Nachdem ein Paar Schuhe zweimal
hintereinander um jeweils 25 % ermäßigt wurden, kosten sie jetzt 54,- €.
Wie teuer waren die Schuhe ursprünglich?
Lösung:
Ansatz:
54,00 €
 75
%
75
%
x
 100
% 100
% |
→
|
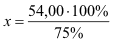 |
→ |
x = 72,00 € |
|
|
72,00 €
 75 %
75 %
x
 100 %
100 % |
→ |
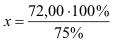
|
→ |
x = 96,00 € |
Die Schuhe kosteten ursprünglich 96,00 €. |
(verminderter
Grundwert)
- Beim Trocknungsprozess von Kamille tritt ein
Flüssigkeitsverlust von ca. 40 % auf. Es bleiben noch 7 kg übrig.
Wie hoch ist der Flüssigkeitsverlust in kg?
Lösung:
Ansatz:
7 kg
 60 %
60 %
x
 40 %
40 % |
→
|
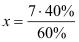 |
→ |
x = 4,7 kg |
Der Flüssigkeitsverlust beim Trocknen beträgt 4,7 kg.. |
(verminderter
Grundwert)
4.
Übungsaufgaben zur
Prozentrechnung
zurück
|