|
Quadratische Gleichungen
[Allgemeine
Form] [Normalform]
[(x
- x1)(x - x2) = 0] [x²
+ q = 0] [x²
+ px = 0]
[Lösungsformel]
[Diskriminante]
1. Begriff:
Eine Gleichung der Form
ax² + bx + c = 0
für a, b, c
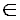
R und a ≠
0 heißt quadratische Gleichung oder Gleichung
zweiten Grades →
allgemeine Form der Gleichung einer
quadratischen Gleichung.
↓
Die Zahlen a, b, c heißen Koeffizienten.
2. Sonderfälle
2.1 Normalform
x² + px + q = 0
ax²
+ bx + c = 0 | : a
→
x² + b/ax + c/a = 0
→
x² + px + q = 0
Merke:Eine Gleichung der Form
x²
+ px + q = 0 heißt Normalform
einer quadratischen Gleichung. (p =
b/a und q =
c/a sowie p, q
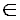
R)
2.2 Gleichung der Form
(x - x1)(x
- x2) = 0
↓
Ein Produkt ist Null, wenn mindestens
1 Faktor Null ist.
x - x1 = 0
x - x2 = 0
→ xI = x1
→ xII = x2
(Zwei Lösungen: (x1, x2)
Merke:
Die quadratische Gleichung (x - x1)(x - x2) = 0 hat genau
2 Lösungen x1 und x2.
Die Faktoren (x - x1) und (x - x2) heißen
Linearfaktoren.
Beispiele:
(1) (x - 3)(x - 7) = 0
(2) (x - 9)(x + 4) = 0
x - 3 = 0
x - 7 = 0
x - 9 = 0 x + 4 = 0
→ x1
= 3 →
x2 = 7
→ x1
= 9 →
x2 = -4
(3) (x + 0,3)(x - 1) = 0
→ Lösungen nur ablesen!
→
x1 = -0,3
→ x2 = 1
(4)
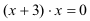 (5) x² = 0 →
(5) x² = 0 →
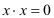
→
x1 = -3
→
x1 = 0
→ x2 = 0 → x2
= 0
2.3 Gleichung der Form
x² + q = 0
Normalform x² + px + q = 0 mit p = 0
→
x² + q = 0
→ x² + q = 0
| -q
→ x² = -q |
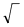
→
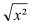 = =
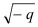
→
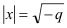
→ 2 Lösungen: +x =
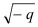 →
x1 = +
→
x1 = +
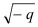
-x = 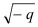 →
x2 = -
→
x2 = -
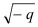
Merke:
Die quadratische Gleichung x² + q = 0 hat nur für q
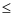
0 Lösungen.
Für q < 0 hat die Gleichung x² + q = 0 genau zwei Lösungen:
x1 = +
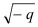 und x2 = -
und x2 = -
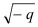 . .
Für q = 0 hat die Gleichung x² + q = 0 genau eine Lösung: x = 0
(Doppellösung x 1 = x 2).
Beispiele:
(1) x² -16 = 0 (→
q = -16 → -q = 16)
→ x1 = 4
x2 = -4
(2) x² + 9 = 0 (→
q = 9 → -q = -9)
→ keine Lösung
(3) x² - 3 = 0
(→ q = -3 → -q =
3)
→ x1 =
Ö3
x2 = -Ö3
2.4 Gleichung der Form
x² + px = 0
Normalform x² + px + q = 0 mit q = 0
→
x² + px = 0
x² + px = 0
↓ x ausklammern!
x(x + p) = 0
↓
↓
x = 0
x + p = 0
→ x1 = 0
→ x2 = -p
Merke:
Die quadratische Gleichung x² + px = 0 hat genau zwei Lösungen: x1
= 0 und x2 = -p.
Beispiele:
(1) x² + 6x = 0
→ x(x + 6) = 0
→ x1 = 0
→ x2 = -6
(2) x² - 3/2x = 0
→ x(x - 3/2) = 0 →
x1 = 0
→
x2 = 3/2
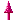
3. Lösung der Normalform einer
quadratischen Gleichung
3.1 Herleitung der allgemeinen
Lösungsformel
x² + px + q = 0
↓ (quadratische
Ergänzung bilden)
x² + px +
(p/2)² - (p/2)²
+ q = 0 | + (p/2)² + q
x² + px + (p/2)² = (p/2)² + q
↓ (Binomische Formel
anwenden)
(x + p/2)² =
(p/2)² + q |
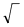
↓ (Gleichung nach x
umformen)
→
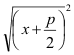 =
=
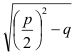
→
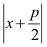 =
=
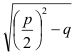
→
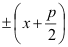 =
=
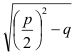 |
|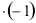 |
|
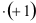
→
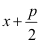 =
=
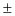 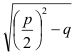 |
|
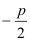
→
x =
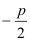 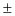 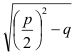
↓
allgemeine Lösungsformel für die
Normalform einer quadratischen Gleichung

3.2
Lösbarkeit quadratischer Gleichungen -
Diskriminante
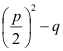 =
= 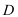 → Diskriminante
→ Diskriminante
Für D gibt es innerhalb
der allgemeinen Lösungsformel für quadratische Gleichungen
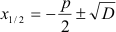 drei Möglichkeiten:
drei Möglichkeiten:
| Fall 1:
D < 0 |
} |
keine Lösung |
|
Radikant D ist negativ |
| Fall 2:
D = 0 |
} |
genau eine Lösung
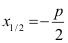
(Doppellösung) |
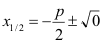 |
| Fall 3:
D > 0 |
} |
genau zwei reelle Lösungen x1 und x2 |
 |
Merke:
Über die Lösbarkeit einer quadratischen Gleichung gibt die
Diskriminante D Auskunft. D =
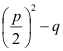 (Normalform)
(Normalform)
D =
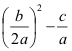 (allgemeine Form)
(allgemeine Form)
Fallunterscheidung:
D > 0 →
Die quadratische Gleichung hat genau 2 reelle Lösungen x1
und x2.
D = 0 →
Die quadratische Gleichung hat genau 1 reelle Doppellösung x = x1
= x2.
D < 0 →
Die quadratische Gleichung hat keine reelle Lösung.
zurück |